img092

a największa wartość siły poprzecznej (rys. 8-4b)

p}_

2

15 6 2

= 45 kN.

Największe wartości naprężeń normalnych w przekroju poprzecznym (rys. 8-4e) — wg wz_0r (8-3):    ^U

bh³

/, = —— (por. tabl. 14-6),

12

yj = y_g = y_mJ'l².

bh³ h bh²    20 • 40²

1T’T“    “

6750

W_r = -

Tnmx = ±

ymax

M_m„,

W,

= +

5333

= 5333 cm³.

6 6 = ± 1,27 kN/cm² = ± 12,7 MPa.

Naprężenia styczne w przekroju poprzecznym (rys. 8-4f) — wg wzoru (8-4): - moment statyczny (zakreskowanej części przekroju)

S

X

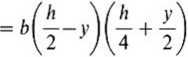
bh²

T~

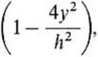
i

- największe wartości naprężeń stycznych w przekroju poprzecznym (gdy V„ = V„_mx)

^m,'^x 8 ^ h²J_3V_muxf 4y²\

I_xb    bh³    2 bh \ h² )

l2^b

Z powyższego widać, że wykres naprężeń stycznych w przekroju poprzecznym prostokątnym belki ma kształt krzywej 2. stopnia. Jeżeli y = ± -j (krawędzie górna i dolna), to

T =

2 bh

= 0,

a gdy y = 0 (oś obojętna), to

3 V

^ ^r HU 2 bh

Po podstawieniu danych otrzymuje się

t = W =    = 0,0844 kN/cm² = 0,844 MPa.

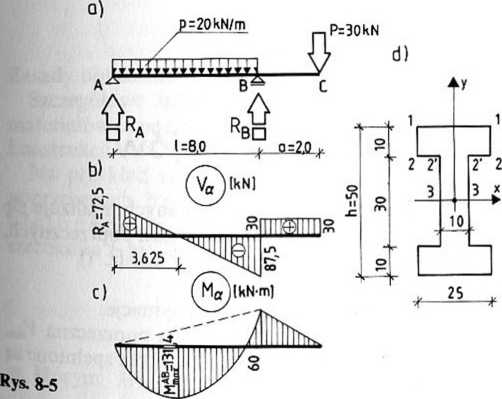
Przykted 8-2. Sporządzić wykresy największych naprężeń normalnych i stycznych ' kroju poprzecznym dwuteowym belki jak na rys. 8-5.

* gnania równowagi:

IY= R_A + R„-pl-P = 0,

ZM„ = R_Al-plO,5l+Pa = 0.

p₀ podstawieniu danych (por. rys. 8-5a) otrzymuje się:

R_a = 72,5 kN,    R„= 117,5 kN.

Największy moment zginający na odcinku AB:

Vr^B = R_a~_Px = 0,    _{x =} ^ ₌ ^ _{= 3},625 m,

A#" =R_ax-^-= 72,5-3,625- ^{20 3}^⁶²⁵ = 131,4 kN -m.

Wykresy K i przedstawiono na rys. 8-5b,c. Z wykresów tych wynika, że w obliczeniach naprężeń należy uwzględnić    87,5 kN oraz M max    131,4 kN • m.

e) f)

£=-1Ł5MPd

= 1^.SMPo

V, =0,772 MPa \ Trr’,93 MPo.

bezwładności przekroju poprzecznego względem osi x (osi obojętnej); rys. 8-5d (por.

/

X

25 • 50³    „ 7,5 ■ 30³

12    “ 12

= 226667 cm⁴.

Wskaźnik

wytrzymałości przekroju na zginanie

W =

226 667

0,5 h

25

= 9067 cm³.