7 (1088)

12

!

siły wypadkowej. Oest to widoczne na rys. I.4b. Rzut siły wypadko* wej W na oś x (OD ) jest równy sumie rzutów na tę oś poszczegól* nych sił składowych (oa'+ a'b' + b'c'-C'd')

i«n

^Wx ’ E ^Plx * ^Plx ^{ł P}2x ^{+ P}3x ^{ł P}4x'

i=l

ponieważ

^Plx	m	^pi	cos	“i	-	30	cos	o o
^P2x	-	^P2	cos	*2	z	20	cos	o o
^P3x	s	^P3	cos *	*3	z	15	cos	240
^P4x	■	^P4	cos	“4	X	25	cos	330

a zatem

w_v • 23 ♦ 6,8 - 7,5 ♦ 21,7 « 44 N.

A

Analogicznie obliczamy rzut wypadkowej W na oś y.

i=n

^Wy ■ Z ^Piy " ^Ply ^{+ P}2y * ^P3y ^{+ P}4y " i=l

P₁ sinor^ + P₂ sina₂ ♦ P^ sinor^ + Pą sinor^ * 30 sin 40°/ ♦ + 20 sin 70° ♦ 15 sin 240° ♦ 25 sin 330° - 12,6 N.

Majęc rzuty W i W wartość wypadkowej W obliczamy z zależności x y

W « /w² + W² . -/44² ♦ 12,6²    « 45,8 N.

Natomiast kierunek działania wypadkowej określić można przez wartość kęta CC, obliczajęc np.

W

tga =    « 3,49206,

y

a kęt CC = 74°0l'.

f

1.1.3. Rozłożyć daną siłę P «■ 30 N na dwie siły, których linie działania będę tworzyć z kierunkiem działania siły P kęty: 0i * 30° 1/9* 40°.

Rozwiązanie

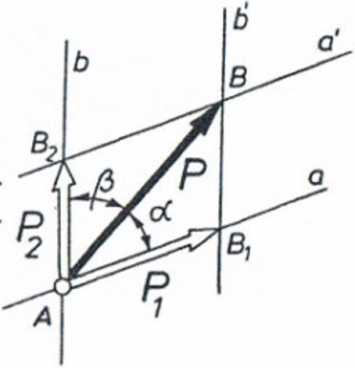
Zagadnienie rozkładu znanej siły P na dwa dane kierunki a i b (rys. 1.5) polega na znalezieniu takich dwóch sił P₁ i P2 wzdłuż prostych a i b, których działanie Jest równoważne działaniu siły P. e więc których sumę geometryczną (wypadkową) jest właśnie siłaP. Można to zapisać równaniem wektorowym

^? - ^pi ♦ V

Wartości sił P₁ i P₂ możemy znaleźć w sposób wykreślny, rysując siłę P w odpowiedniej podziałce (rys. 1.5) oraz pro wadząc przez punkt A, będący punktem przy łożenia siły P, proste a i b (kierunki działania sił składowych).Następnie kreśląc przez punkt B, który jest końcem wektcra P, proste a'i b'równoległe odpowiednio do kierunków a i b, otrzymujemy    Rys. 1.5

punkty 8^ i B₂ wyznaczające szukane wektory składowe P^^ i P^.

Wartości składowych P^ i P^ możemy również wyznaczyć analitycznie rozwiązując jeden z otrzymanych trójkątów, np. trójkąt ABB^•

2 twierdzenia sinusów otrzymujemy

^ABi

sin/3

^B1^B

AB

^sln“ sin [l80° - (oć ₊ /3 )]

Z powyższych związków otrzymujemy

P

sin/3

sin (ar ♦ >3 ) '

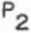
o sin oc ^p sin( or ♦ /i)'

a po podstawieniu danych liczbowych

30

sin 70

sin 40

.20,5 N,

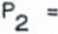
sin 30° sin 70°

16 N.