jopek

Imię <

W metodzie SMARTER wagi wyliczane %ą na podstawie [ A T irtdnlt) i opinii ekspertów 1 B | metody rot r

wag Ictóre podał decydent _t

Kolp|no<ć d/iałań w danym procesie i jednoczesna zależność między elementami systemu z naciskiem na kolejność działań reprezentuje:

rtkrrui A*(?J,9J) rostał znormalizowany do przedziału A'«f l.S) ri*m»ntnv»i o * .r będłl* odpowiada! elementy ze zbioru A' o wartości

^Ą I ^{1 5}    __f B [TT

lA | Drzewo decyzyjne [ B | Schemat funkcjonalny C_ Schemat sekwencyjny [ 0 [ Schemt współdziałanie

C AHP

i D ^ PPOMgTHggll

Metody wielokryterialnego wspomagania decyzji me jest: ! A fsMART ~~

B

MTBF

Stosując kryterium Maxl Min, do poniższej tabeli, wskaż który wariant zostanie najlepiej oceniony

		Stan natury SI	Stan natury S2	Stan natury S3
A	Wariant 1	100	100	400
B	Wariant 2	-200	150	600
C	Wariant 3	0	200	500
D	Wariant 4	100	300	200

6. Współczynnik występujący w kryterium Hurwicza to współczynnik:

A niespójności

B

zgodności

C

optymizmu O niepewności

7. Kryterium podejmowania decyzji w warunkach nieznanego ryzyka NIE jest kryterium

A	Hurwicza	B	Laplace'a	C	Savage	D	Wartości oczekiwanej
Odległość pomiędzy punktami A(3,-2,5) i B(3,l,-7) w metryce cityblock (Manhattan) wynosi
A	5	B	12	C	5.7	D	15
1270zł umieszczono na 3 lata		na lokacie o rocznym oprocentowaniu 4%. Po 3 latach kwota wraz z odsetkami wyniesie
A	1587.5	B	1428.6	C	1320.8	D	1123.6
Rzeczywista stopa oprocentowania przy nominalnej stopie oprocentowania 12% i inflacji równej 4 % wynosi:
A 1	7.69%	B	8.12%	C	8.0%	D	1.6%
---- Praktycznie stosowaną miarą niezawodności jest współczynnik:
^A1	naprawialności	B	gotowości	C	Intensywności awarii	JjL	| zastępowalności

12. Jeżeli Ri=0.8, R2=0.9, R3=0.7 R4=0.8 to niezawodność układu przedstawionego na rysunku wynosi:

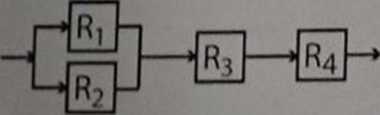
A

0.61

B

0.988

U

0.77

D 0.55

13. Niezawodność systemu wynosi Rs=RiR2R3+RiR4+R3R5-RiR2R3R4-RiR3R4R5-RiR2R3Rs+RiR2R3R4Rs. Zakładając ze Ri=R2=0.8 a r₃=r₄=r_s=0.9, niezawodność którego elementu należy poprawić, by najbardziej poprawić niezawodność układu?

Lą_

R1

B

R2

C

R3

D ! R4

14. W metodzie AHP w pustej kratce macierzy preferencji powinna się znaleźć liczba

	R1	R2
R1	1	3
R2		1