KONSTRUKCJE STALOWE STR108

1

108

5.11. Zginanie z siłą podłużną

Procedura 5.7. Uwzględnianie wpływu siły podłużnej na nośność przekroju przy zginaniu

Formuły

Objaśnienia

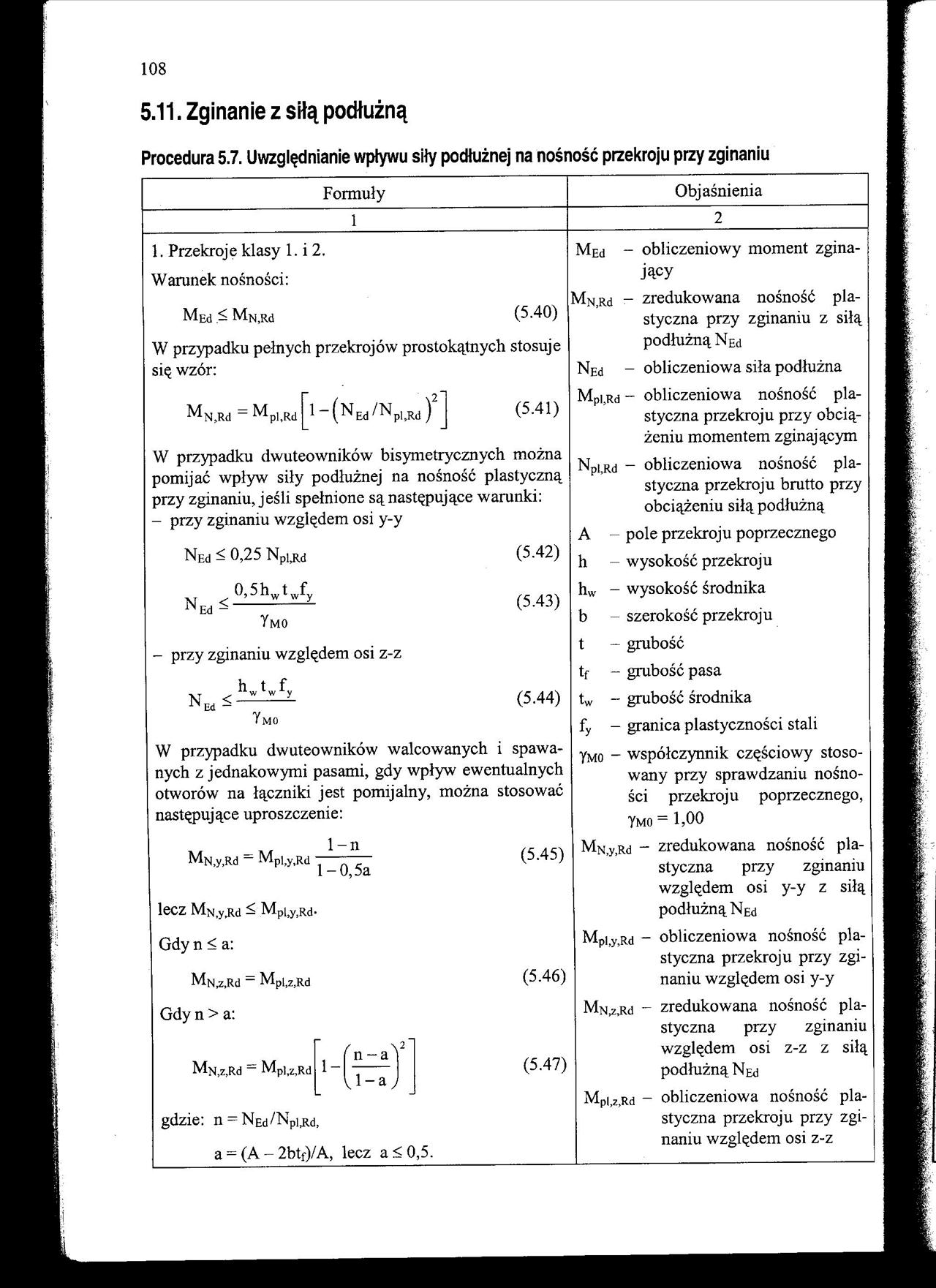
1. Przekroje klasy 1. i 2.

Warunek nośności:

Mtd <    (5.40)

W przypadku pełnych przekrojów prostokątnych stosuje się wzór:

2

Mn,r<i - M_{pl Rd}

l-(N_M/N_pl,_Rd)'

(5.41)

W przypadku dwuteowników bisymetrycznych można pomijać wpływ siły podłużnej na nośność plastyczną przy zginaniu, jeśli spełnione są następujące warunki:

- przy zginaniu względem osi y-y

Ne<j ^ 0,25 Npijui 0,5h_wt_wf_y

(5.42)

N_Ed^

Ymo

(5.43)

przy zginaniu względem osi z-z htf.

N_m<

w w y

Ymo

(5.44)

W przypadku dwuteowników walcowanych i spawanych z jednakowymi pasami, gdy wpływ ewentualnych otworów na łączniki jest pomijalny, można stosować następujące uproszczenie:

MN.y.Rd - Mp|_>y,Rd

lecz MN,y,Rd ^ Mp[_>y>Rd. Gdy n < a:

M_N^,Rd - M_p[_jZ;Rd Gdy n > a:

MN,z,Rd “ Mp)_iZ,Rd

1-n

1 -0,5a

(5.45)

(5.46)

1-

^/n -a^²

V

1-a

gdzie: n = N_Ed/N_pi^_dj

a = (A - 2btf)/A, lecz a < 0,5

(5.47)

M_Ed - obliczeniowy moment zgina- i jacy    '

M»_;Rd - zredukowana nośność plastyczna przy zginaniu z siłą podłużną N_Ed

N_Ed - obliczeniowa siła podłużna

Mpi_;R_d - obliczeniowa nośność plastyczna przekroju przy obciążeniu momentem zginającym

N_pi,Rd - obliczeniowa nośność plastyczna przekroju brutto przy obciążeniu siłą podłużną

A - pole przekroju poprzecznego

h - wysokość przekroju

h_w - wysokość środnika

b - szerokość przekroju

t - grubość

tf - grubość pasa

t_w - grubość środnika

f_y - granica plastyczności stali

Ymo - współczynnik częściowy stosowany przy sprawdzaniu nośności przekroju poprzecznego, Ymo = 1,00

Mu.y.Rd - zredukowana nośność plastyczna przy zginaniu względem osi y-y z siłą podłużną N_Ed

Mpi_>y>R_d - obliczeniowa nośność plastyczna przekroju przy zginaniu względem osi y-y

MN,z,Rd - zredukowana nośność plastyczna przy zginaniu względem osi z-z z siłą podłużną Neo

M_pi_iZ,Rd - obliczeniowa nośność plastyczna przekroju przy zginaniu względem osi z-z