lastscan15

2.2. Zasada dyskonta handlowego

Jeśli opłatą za pożyczkę jest dyskonto D. to po jego zapłaceniu w chwili otrzymania pożyczki dłużnikowi pozostaje kwota

(2.1)

P = F—D.

Pożyczka ma sens oczywiście tylko wtedy, gdy P > 0, zatem dla dalszych rozważań należy dodatkowo założyć, że D < F. W sytuacji, gdy dana jest wartość końcowa F, czas n, na który udzielono pożyczki, oraz stopa dyskontowa d, w celu obliczenia dyskonta D korzystamy z następującej zasady.

Zasada dyskonta (handlowego prostego)

Dyskonto jest obliczane od kwoty, którą dłużnik zwróci po ustalonym czasie, jest proporcjonalne do tego czasu i jest odejmowane od tej kwoty w chwili

udzielenia pożyczki.

Zgodnie z powyższą zasadą dyskonto D od kwoty F za czas n przy danej stopie d oblicza się jako

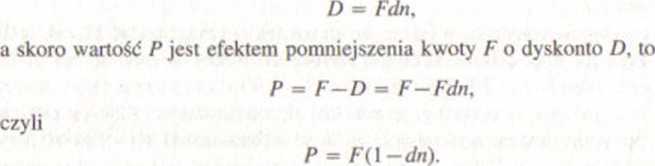
120

(2.2)

(2.3)

1 "

d= 15%

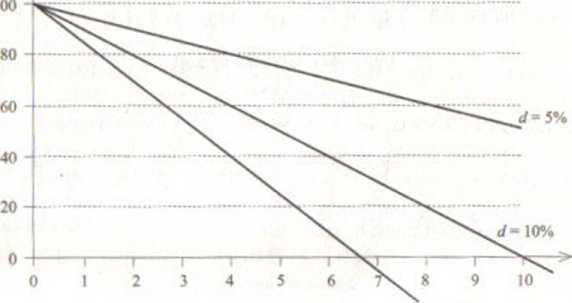
Rysunek 2.2. Wartość początkowa /‘jako liniowa funkcja czuu dyskontowania n

Równ.im.i iJ 2)    nazywamy ni.»<lrl*iti ayRHonw

Z postaci równania (2.3) wynikają następujące wnioski (ich ilustrucja jest rysunek 2.2):

•    wartość /* jest liniową funkcją czasu dyskontowania n;

•    przy F > 0 oraz d > 0 jest to funkcja malejąca;

•    roczny spadek wartości tej funkcji jest równy rocznemu dyskontu, które wynosi D = Fd\

•    przy ustalonej wartości F ta funkcja maleje tym szybciej, im większa jest stopa d,

• wartości tej funkcji są dodatnie tylko dla czasu dyskontowania mniejszego ixl pewnej wartości n (rozpatrzeniem tego problemu zajmujemy się nieco dalej, po zakończeniu przykładu 2.3).

Z modelu dyskonta wynikają następujące zależności, użyteczne dla dalszych rozważań

^F= !-*•	(2.4)
	(2.5)
D " “ Td'	(2.6)

Przykład 2.2

Aby dziś dostać pożyczkę, zobowiązujemy się oddać po 3 miesiącach 1500 zł. Jeśli opłata za pożyczkę ma postać dyskonta obliczanego przy stopie d = 14%, to lnie ze wzorem (2.2) wyniesie

D = 1500 0.14 — = 52.5 zł

i dziś. po jej potrąceniu, dostaniemy

P = F-D = 1500-52,5 = 1447,5 zł.

Aby dowiedzieć się, ile trzeba by oddać po 3 miesiącach, chcąc obecnie stać 1500 zł. korzystamy z wzoru (2.4), z którego wynika, że

1500

1 -dn 0.965

= 1554.40 zł.

Z kolei, gdyby dziś otrzymane 1500 zł mogło być spłacone za 4 miesiące kwotą 1560 zł, to „ceną” pożyczki byłaby stopa dyskontowa o wysokości obliczonej według wzoru (2.5),

d =

- = 11.54%.

60

¹⁵⁶⁰-nr

39