MATEMATYKA 4

POLA I OBJĘTOŚCI FIGUR

Koło

Q

F =7Tr² S = 27Tr d = 2r

Prostopadłościan V=abc <*1 l~d=Va²+b²+c²' F=2(ab+ac+bc]

Stożek ścięty _t±fV='^(R²+Rr+r²| _ _³P=tT(R+r)l F=TTr(l+r)+ +7TR(I+R|

Odcinek kołowy F₌TTRfa (R-h| ^pr-H 360°

^R^=l^lfc^nal

Równoległościan

t

h V = F,h

i

Walec

V = TTr²h P= 27Trh F = 2TTr|r+h)

Wycinek kołowy TTr²a

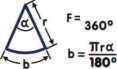
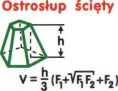
Ostrosłup

t .

hv ₌ l_F,h

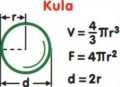
Odcinek kuli V='?Ł|l(3r²+h²)

tiTl'

l?V=^l*3R-h)

P= 2TTRh

Wycinek kuli

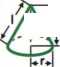
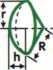
V = |lTR²h

F=7TR(2h+r)

Sześcian

SP

-a-*ł*a d=aVz

Stożek kołowy

r \ T V= V²h iVp=»rl

F=TTr(l+r)

F_ł i F₂-pola podstaw, TT = 3,14...

S- obwód, F- pole powierzchni całkowitej, P- pole powierzchni bocznej, V - objętość,

WZORY TRYGONOMETRYCZNE

B	90°-a	»0°+a	i80°-a	l80°+a	270°-a	270°+a	360°-a
sin P	cosa	cosa	sina	-sina	-cosa	-cosa	-sina
cosP	sina	-sina	-cosa	-cosa	-sina	sina	cosa
tgB	ctgct	-ctga	-tga	tga	ctga	-ctga	-tga
ctgB	tga	-tga	-ctga	ctga	tga	-tga	-ctga

sin^za+cos^za = l tga-ctga = l tga

. sina ' cos a

ctga

cos a ' sina

sin(a+B) = sinacosP±cosasinP cos(a+P) = cosacosB+sinasinB sin2a = 2sinacosa

cos2a = cos²a-sin²a • « 2tga _ i-tg²a _x 2tga . ctg²a-i

sin2a=, ³ cos2a =-—    tg2tt =    *    ctg2a= . „

i+tg²a    i+ta²a    l-tg²a    ³    2 ctga

tg|<X±B| = ^{t9fltt9B 91}    l + tgatgp

_ctg(atB)=E!gąEM±2

ctgp+ctga

l+tg²a

l+cosa=2cos²^

n² —

a . /j+cosa' 2 ⁼-*»    2

„a _+ rr

'2 ^=tv—

cosa

sin

t_g« ₌ + J___

cosacosp ³ 2    " Yi+cosa l+cosa

sin(atP)

tga+tgP =

ctga±ctgB=:    ctgS =±JJięosćl

^{3    3} sinasin (3    2 V 1-cosa

1-cosa _ sina _ 1-cosa sina

1+cosa _ sina

sina+sin6=2sin?±2cos2d*

Since- sinB = 2cos^sin ^

_ _ <x+B Ct-P cos a+cos P=2cos-2~ cos-y

sina 1-cosa

a	(0°90°	(90°,180°)	(180?270°)	(270?360°)
sina	+	+	-	-
cosa	+	-	-	+
tga	+	-	+	-
ctga	+	-	+	-

cosa-cosP = -2sin^ysiny

a	0°	15°	30°	45°	o* O o	75°	90"	180°	270°	360°
sina	0	V6V2- 4 j	1 2	2	VT T	VóV/T 4	1	0	-1	0
cosa	1	4		VI 2	1 2	V6-V? 4	0	-1	0	1
tga	0	2-V?	V? T	1	V5	2+vr	+ oo	0	too	0
ctga	+oo	2+V3		1	3	2-V3*	0	+o°	0	+ oo