materialy str1

Materiały do ćwiczeń z przedmiotu Prognozowanie i symulacje -11 semestr SUM studia zaoczne

TREND POTĘGOWY

Zadanie 3; Tabela przedstawia dane dotyczące liczby martwych urodzeń na 1000 urodzeń w Polsce w latach 1997 - 2003:

rok	1997	1998	1999	2000	2001	2002	2003
t
y,	10,7	10,2	9,9	9,9	9,7	9,3	9,2

1.    Oszacuj parametry potęgowej funkcji trendu.

2.    Dokonaj oceny zgodności danych empirycznych z danymi wynikającymi z oszacowanej funkcji trendu na podstawie ocen parametrów struktury stochastycznej, tj. odchylenia standardowego reszt, współczynnika zmienności reszt, współczynnika zbieżności i współczynnika determinacji liniowej.

3.    Zbadaj istotność parametrów funkcji trendu.

4.    Wyznacz prognozy punktowe na 2004 i 2005 rok.

5.    Sprawdź dopuszczalność prognoz punktowych miernikami ex antę.

6.    Wyznacz prognozy przedziałowe na 2004 i 2005 rok z wiarygodnością 95%.

7.    Oceń dopuszczalność prognoz przedziałowych miernikami ex antę.

Rozwiązanie:

Ad. 1. Szacowana funkcja trendu jest funkcją potęgową postaci: f(f) = a₀t^a' .

Zapis macierzowy - rozdział 3.3. wzory: (3.10) - (3.49)

~ y i ~ _	an		lna0
(xxj X'y =	U	=	u
			. ^ai .

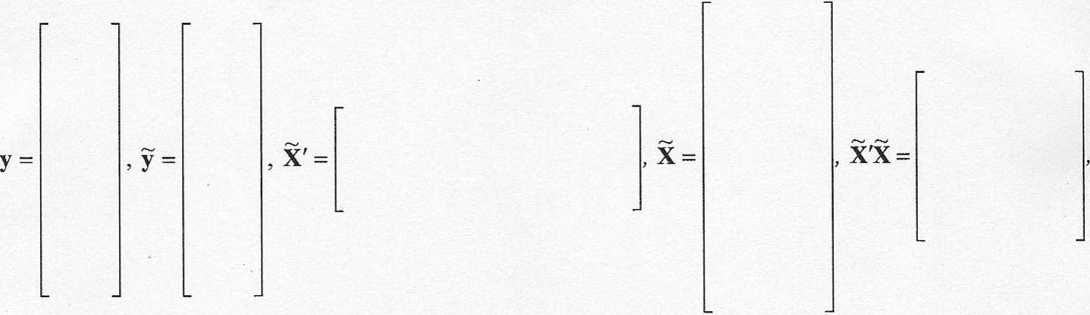
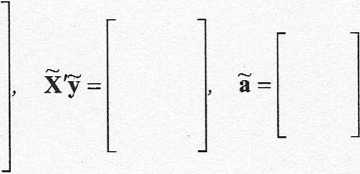
det(x’x)=    , (x'x)”' =

Oszacowana liniowa funkcja ma postać:

Oszacowana potęgowa funkcja trendu ma postać:

Ad. 2. Miary dopasowania:

₉    i*⁷ Ci

•    Wariancja resz: ?_e² =- =0,000196

n-2

•    Odchylenie standardowe reszt: 7_e =    = 0,0140

Strona 8 z 12