md kolos

1. Dzieci podczas zabawy dobierając się w k grup, przy czym podczas każdej zabawy tworzą inne k grup (podział na grupy inny od poprzednich). Zabawa kończy się, gdy wyczerpią się możliwości utworzenie k grup. Ile rund bawiły się dzieci, zakładając, że było ich n? Znaleźć zależność rekurencyjną. Zakładamy, że są możliwe grupy jednoosobowe. Wyliczyć wartości dla n,k < 8 (w postaci tabelki).
2. Liczba funkcji ze zbioru n elementowego w zbiór m elementowy wynosi mn. Jak wiele z nich ma więcej niż k różnych wartości? Zakładamy, że k < min(n, m).
3. Dzieci podczas zabawy dobierając się w k grup. Każda grupa następnie tworzy kółko i trzymając się za ręce dzieci zaczynają tańczyć. Na ile sposobów n dzieci może utworzyć się k kółek? Kolejność dzieci w kółku ma znaczenie. Zakładamy, że są możliwe kółka jednoosobowe. Wyliczyć wartości dla n,k < 7 (w postaci tabelki).
4. Dzieci mają 15 różnokolorowych piłek (piłki są rozróżnialne) oraz nieograniczoną liczbę jednakowych koszyków (koszyki są nierozróżnialne). Podczas zabawy przekładają piłki między koszykami, ale w taki sposób, że zawsze na koniec każda piłka jest w jakimś koszyku, ale niektóre koszyki mogą być puste. Na ile sposobów mogą powkładać 15 piłek do koszyków? Na ile sposobów mogą powkładać n piłek do koszyków? Wyprowadzić zależność rekurencyjną.
5. Mamy obliczyć iloczyn 4 macierzy Ax * A2*A3* A4. Zakładamy, że wymiary macierzy są odpowiednie i mnożenie jest wykonywalne. Kolejność mnożenia macierzy wpływa na czas mnożenia macierzy (liczba wykonanych operacji). A ile sposobów można wykonać mnożenie 4 macierzy (kolejność wykonywania mnożeń, liczba sposobów wstawienia nawiasów)? Ile będzie sposobów mnożenia macierzy dla 5,7 lub n macierzy?
6. Ile mamy rozwiązań równania diofantycznego: xx + x2 + x3 + x4 = 11, gdzie
xx < x2 < x3 < x4 oraz xt e P?
7. Znamy rozwiązanie dla problemu kraty z przekątną. Wiemy, że liczba sposobów, na które można przejść po kracie n xn (kwadratowej) z lewego dolnego wierzchołka do prawego górnego wierzchołka w ten sposób, że można poruszać się tylko w prawo bądź do góry i nie można przekroczyć przekątnej łączącej dwa przeciwległe wierzchołki, wyraża się n - tą liczbą Catalana. Wykorzystując tą zależność dowiedz, że:
n-l
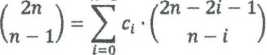
Wyszukiwarka
Podobne podstrony:
Image512 emiterowego RE. Po przełączeniu na wyjściu układu pojawia się sygnał 1, przy czym sygnał te
IMAG1304 pomieszczeniu, 1 którym pacjent się znajduje, przy czym: 1) wiązkę pierwo
stawały się lżejsze. Przy czym co ważne wymiana odbywała się w proporcjach 7 starych za 6 nowych den
P040311 51 w tk b e {0.1} repie/entację dziesiętną otrzymuje się jako L{B) * y /&
324 (35) - 324Tranzystor bipolarny otrzymuje się = --- (5.150) 1 4--— r r przy czy
teatr28 dzi". Tak w dawnej Polsce rozpatrywano kwestię osoby nowo pojawiającej się w towarzystw
zdj cie0249 Zad. 16. W temperaturze 27°C 8 g tlenu pod ciśnieniem 10,13 1Q5 N/m2 rozszerza się adiab
zdj cie0250 Zad. 16. W temperaturze 27°C 8 g tlenu pod ciśnieniem 10,1310 N/nr rozszerza się adiaba
71393 Obraz!0 (11) Wyprawę narzuca się dwukrotnie, przy czym drugi raz dopiero po wyschnięciu pierws
Image512 emiterowego RE. Po przełączeniu na wyjściu układu pojawia się sygnał 1, przy czym sygnał te
Img00127 131 i związków, które stają się nadprzewodnikami, przy czym stale odkrywane są coraz lo now
Próbki umieszczone w pierścieniu edometru obciąża się stopniowo przy czym każde kolejne obciążenie j
P1100260 przypadku pojawia się maksimum, przy czym ^ odpowiada wartości dla oętZT nie aktywnego pasm
DSCN6306 (Kopiowanie) DNA: jedna z nich kończy się sekwencją -A-A-T-T-C (przy czym odcinek A-A-T-T j
więcej podobnych podstron