mech2 85

1CU

r 2)

Uwagą: Wzór określający ^J można otrzymać również z wzorów trans-, f ormaoyjnyob.

I

Y W²,

Mr‘

<L    • cL    P

!p = OOB a + I^’cos P + I_zz 003 y - 21 cos a cos 0 -

•I

- 21^' coa acosy - 2Iy_z cosg cosy

W przypadku oznaczeń jak na rysunku i02ot

2

u r

^ ⁼ °* ^Izz ⁼ °* -^yy ⁼    5

Po podstawieniu

0 = 90° -a , _Y = 90°-

Ip = —y oos² (90 - a) =

M l^c . 2 —2— ein a .

Zadanie 2 (ryB. 103)

Wyznaczyć momenty "bezwładności jednorodnej cienkiej tarczy okrągłej promieniu r i masie M względem jej środka O i średnicy.

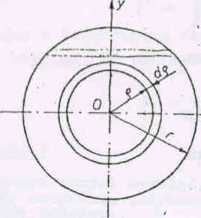
Rys. 103

ły

2 zależności między momentami bezwładności względem osi i względem pur tu będącego początkiem układu otrzymamy

I.

I_ = i™ ^c ~jr 1

xx TI

M r‘

i Wyznaczmy promień bezwładności względem średnicy

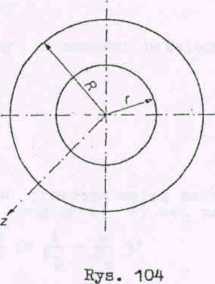
Zadanie 3 (rys. 104)

Wyznaczyć moment bezwładności jednorodnego oienkiego pierścienia masie M, promieniu wewnętrznym r i zewnętrznym R względem osi metrii.

°ap.    j!ł

Zadanie 4 (rys. 105)

Wyznaczyć moment bezwładności względem prostej p układu ełożon

” -------------------■*—t.-■>. — •< „ -<«

n v i<uau łjj w. mjouju u «    --------------u— _%_____ _K____ _ _w

z pręta o długości 1 i masie M. oraz przymocowanego pierścienia jed rodnego 0 masie M2 i promieniu R. Założyć, że wymiary przekroju porr* nego pierścienia w stosunku do dJ oraz wymiary poprzeczne pręta w stos ku do 1 są tak małe, że mogą być pominięte.

. Rozwiązanie

^J0 ¹ i

2

p dm,

dm = y 2u p dp.

Y - gęstość jednostki powierzchni r

j 2 ny P³ d p = 2n y J P⁴

71 y _r

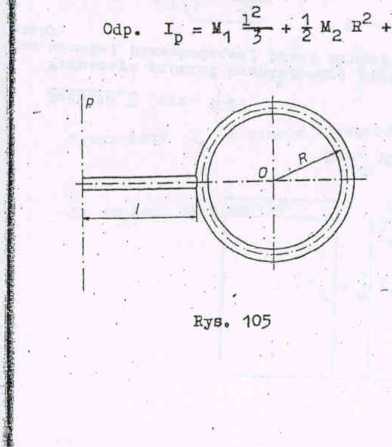
M„ R² + M~(l + R).

i