mechanika15

Przy próbie przesunięcia tarczy za pomocą poziomej siły P pojawia się rozłożona siła tarcia, którą zastępujemy siłą skupioną T (rys. I.36b). W stanie równowagi granicznej słuszne jest prawo Coulomba:

T • pN, 0 < p < l    (1.48)

gdzie p jest współczynnikiem tarcia ślizgowego (statycznego rozwiniętego). Po przekroczeniu równowagi granicznej następuje ruch ciała w kierunku dzia łania siły P. Siła tarcia ma zwrot przeciwny do siły P.

Układ sił działających na tarczę traktuje się w przybliżeniu jako płaski zbieżny układ sil. W stanie równowagi granicznej spełnione są 2RRS:

(1.49)

X = 0: P-T • 0 =* P = T 53^ = 0: N-Q = 0=>N = Q Po uwzględnieniu T = pN = pQ, otrzymuje się

P - P_v -    (1^50)

Kąt tarcia (p jest zdefiniowany związkiem

P ■ tg<p    (1.51)

Siłę przesuwającą P - P wyznaczamy indywidualnie w danej konfiguracji.

o*

Tarcie toczne (opór toczenia)

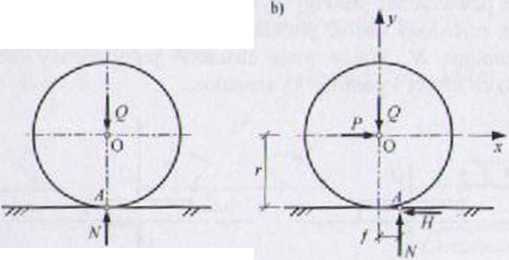
Rozpatrujemy ciało sztywne typu walec, kula, baryłka. Płaskim modelem takiego ciała jest krążek o promieniu r (rys. 1.37a). Ciężar krążka Q jest zrównoważony przez rozłożony nacisk podłoża na tarczę. Nacisk rozłożony zastępujemy siła skupioną N Więzy mają charakter jednostronny nicidculny

30

Rys. 1J7

Statyka Podstawy icorciycMW

I*i/\ próbie przetoczenia krezka za pomocą poziomej siły P pojawia się flfffiimięcic teoretycznego punktu podparcia A w kierunku działania siły P «/ !»• •chylenie reakcji podłoża o składowych //, N (rys. 1.37b). W stanie łrtniM-w.igi granicznej przesunięcie / punktu A jest największe. Wielkość / Mow.i N«e ramieniem oporu toczenia. Po przekroczeniu równowagi granicznej mt Kpiąc toczenie się krążka w kierunku działania siły P.

i H ul sił działających na krążek jest płaskim układem sił. W stanie równo-JMyi granicznej spełnione są 3RRS:

= 0:    />-// = 0 =*// = P

E^Y = 0:    ^N~Q =0 -t N = O    _(|52)

£Af_o=0: Nf - Hr - 0 => P - P_p - Q l NS .inmek toczenia ma postać:

H < T = \iN    (1.53)

i l i / jest silą tarcia ślizgowego. W przeciwnym przypadku nastąpi poślizg • tą/ka.

W niektórych układach P_p można wyznaczyć bezpośrednio z równania

0: Qf-Pr = 0 -»/> = />,,- <?•£    (1.54)

Sili. P _t oraz reakcje H wyznaczamy indywidualnie w danej konfiguracji.

I .ii i ie cięgna o krążek

i ięgno (pas. lina) jest elementem wiotkim, przenoszącym tylko silę rozciąga-lui i W mechanice ogólnej zakłada się, że cięgno jest nieodksztalcalne (nie ulega wydłużeniu). Prostoliniowy odcinek cięgna zachowuje się jak więź elementarny i wciągany. Cięgno przełożone przez krążek (lub owinięte o krążek) przyjmuje 1 ./tali krążka. Krążek zmienia kierunek siły przenoszonej przez cięgno.

Przy próbie przesunięcia napiętego cięgna przełożonego przez nieruchomy kią/ck naciągi cięgna są różne po obu stronach krążka (rys. 1.38a). Zależność między siłami P i R ma postać

P=e“^BP    (1.55)

lub odwrotnie

R = t~*^mP    (1.56)

gdzie: p - współczynnik tarcia ślizgowego cięgna o krążek, a [rad) - kąt opasania.

W zagadnieniu odwrotnym rozpatruje się próbę obrotu krążka podpartego przegubowo względem nieruchomego i napiętego cięgna przełożonego przez

31

Statyku. Podstawy teoicty«./nc