mechanika4

Moduł (wartość) wektora a wynosi

a - yo* ♦ Qy ♦ flj    (12)

ponieważ wektor a jest przekątną prostopadłościanu rozpiętego na rzutach. Kosinusy kierunkowe wektora a wynoszą

«*

cos a = — a

cos² a.

cos²a ♦ cos²a.

(1.3)

o,

cos a = — ^r a

cos o. ■ — a

Dowolnej osi u w przestrzeni przyporządkowany jest wcrsor e_¥, którego składowe w układzie xyz możjia obliczyć na podstawie wektora geometrycznego na tej osi. o zwrocie zgodnym ze zwrotem wersora (rys. 1.2):

P ⁼ pa ⁺ Pj«, ⁺ pA

*M^m*A-*B»    p,-y_A-y_B« p, =Za'^B

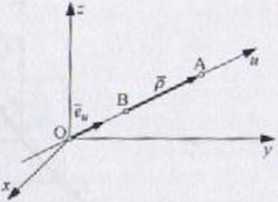
Rys. 1.2

Wówczas, zapis analityczny wersom e ma postać:

(1.5)

ee+ee+ee

>y kzz

gdzie

P = y'p* * pJ * pJ

(1.6)

UsM./nmmy wektory swobodne, liniowe i zaczepione. Wektor swobodny JH! określony przez wartość, zwrot i kierunek. Może być on przesuwany idwooli i le (rys. I3a). Wektor liniowy jest określony przez wartość, zwrot i |mi•.11 działania (rys. I.3b). Wektor zaczepiony jest określony przez wartość, #1*1. i («• i działania i punkt zaczepienia (rys. I.3c).

■i

bi

Rys. I 3

/iniiiiui zwrotu wektora jest równoważna ze zmiana znaku:

(1.7)

b = -a = -a e - n e - a e xx y y z z

'••nu i dwóch wektorów jest określona wzorami:

(1.8)

ć = a * b - c_xe_a+ c_yt_y * c.e.

^c,^{m    C}j'^ay + ^b,' ^ci ^{= a}z+^b'

Wrktoi ć jest przekątna równolegloboku rozpiętego na wektorach a, b. jeśli w .hory a. b *4 narysowane w obranej skali. rys. I.4a.

Rys. t.4

Wartość wektora r można obliczyć ze wzoru

(1.9)

ri 2    2

<* “ V^c< ⁺ c_f ♦ c_z

AliiWk' IVdsUiwv l.-.M. iyi/n. 9