mechanika84

/.adanie 2Ji

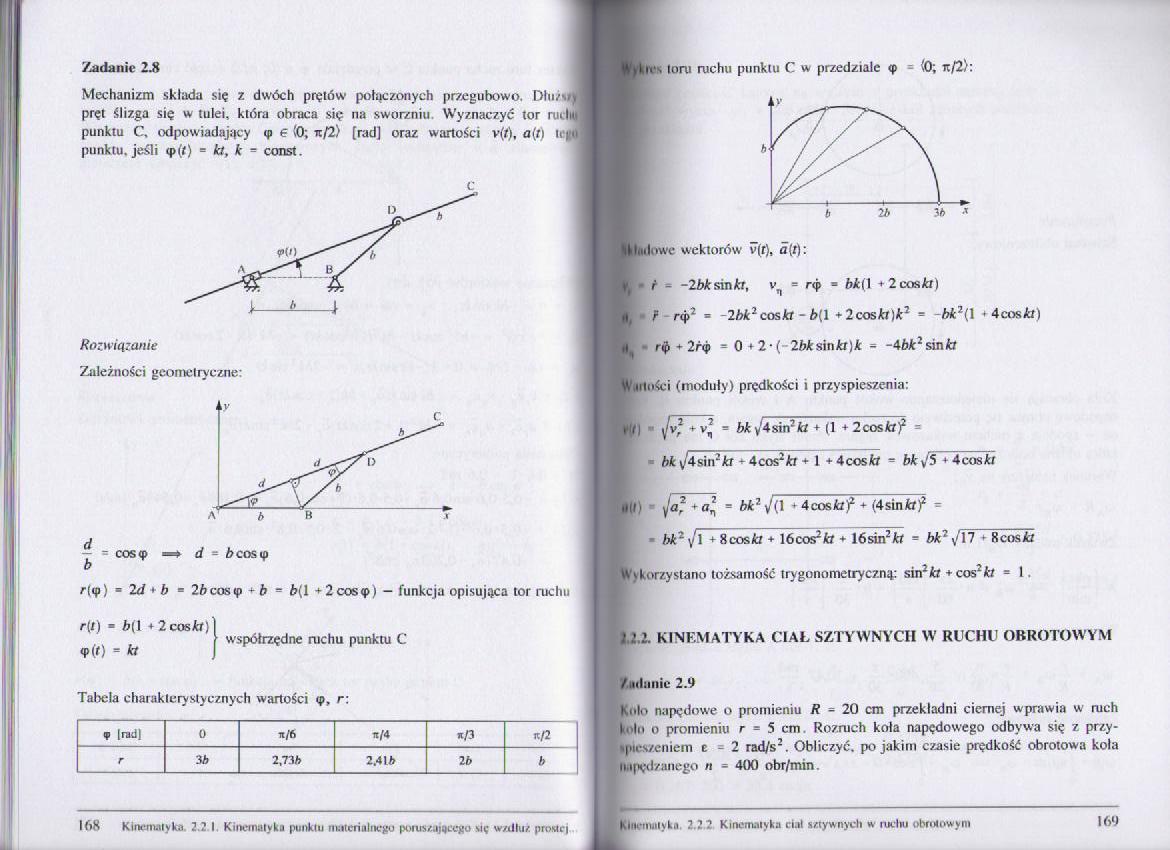
Mechanizm składa się z dwóch prętów połączonych przegubowo. Dłu/w) pręt ślizga się w tulei, która obraca się na sworzniu. Wyznaczyć tor rudni punktu C, odpowiadający cp € (0; k/2> [rad] oraz wartości v(t), a(t) ti j < punktu, jeśli <p(f) = la, k = const.

C

Rozwiązanie

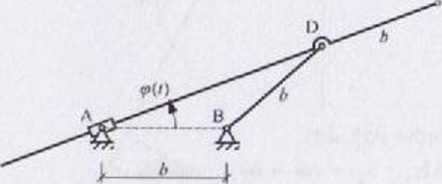
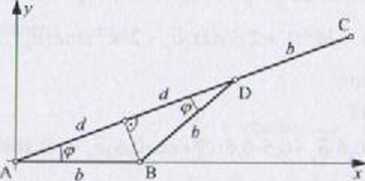
Zależności geometryczne:

d

— sr

b

'(9)

r(t) ■ 9(0

cosep —» d = b cos ip

■ 2d * b » 26cos«p + b = b{ 1 + 2cosq>) - funkcja opisująca tor ruchu b{\ *2 coskt) I

[ współrzędne ruchu punktu C

Tabela charakterystycznych wartości q>, r:

<P |radl	0	n/6	n/4	k/3	*/2
r	3 b	2,73 b	2.4 Ib	Ib	b

I6K Kinematyka 2.2 I. Kinematyka punktu materialnego poruszającego się wzdłuż prostej

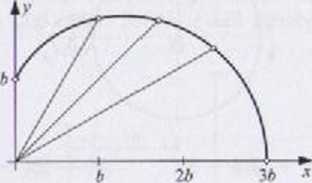
t||ii,it|.iwo wektorów v(r), a(/):

k - f - -2bksmkt, v_tj = r<p ■ M(1 + 2cos£r) jt. - r rą>' = -2M²cosAr -b[\ + 2coskt)k⁷ = -bk²( 1 « 4coskt)

* ^r$ ♦ 2r<p = 0 + 2*( 2b*sinJfcr)A: = -4bk² sinb

IV,uliisci (moduły) prędkości i przyspieszenia:

i f ^f \jv* ⁺ \ - bk^4 sin² kt + (1 + 2cosktf =

bk _v'4sin²Jtr + 4cos²*/ + 1 + 4cosfa = bkJŚ * 4coski

fe(f)    y'a? + a* = bk² ^(1 * 4cosktf + (4sinkt? -

hk^z yl ⁺ 8cosfo ♦ lócos²/^ ♦ 16sin²fa = M^? y 17 ♦ Rcosto Skorzystano tożsamość trygonometryczną: sin² to + cos^:fo = 1.

: * 2. KINEMATYKA CIAŁ SZTYWNYCH W RUCHU OBROTOWYM / .ulanie 2.9

Kolo napędowe o promieniu R = 20 cm przekładni ciernej wprawia w ruch kolo o promieniu r » 5 cm. Rozruch kola napędowego odbywa się z przy-i u s/cniem t - 2 rad/s². Obliczyć, po jakim czasie prędkość obrotowa kola napędzanego n = 400 obr/min.

169

MfkMittiiyko 2.2 2 Kinematyka cl.it sztywnych w ruchu obrotowym