Resize of Resize of Scan0001

/

SAD - egzamin 8 lipca 2002

Tl

Nr grupy:

Imię i nazwisko:

Zadanie 1. (6 pkt.) 70 procent pracowników pewnej firmy ma miesięczny dochód przewyższający średni dochód miesięczny w kraju. Obliczyć przybliżone prawdopodobieństwo, że wśród 60-ciu losowo wybranych pracowników co najmniej 40 osób będzie miało dochód przewyższający średnią krajową.

Zadanie 2. (6 pkt.) Ceny pudelka dyskietek (danej firmy) w sześciu losowo wybranych sklepach wynosiły (w zl):

10,00 9,50 12,00 12,00 12,50 10,00.

Zakładając, że rozkład ceny jest normalny zbudować 95-procentowy przedział ufności dla wartości średniej ceny.

Zadanie 3. Niech będą dane zmienne losowe X i Y o łącznej gęstości danej wzorem

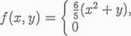
dla 0 < x < 1, 0 < y < 1 w przypadku przeciwnym.

(a)    (3 pkt.) Znaleźć gęstości brzegowe jx, fy-

(b)    (1 pkt.) Czy X i Y są niezależnymi zmiennymi losowymi?

(c)    (2 pkt.) Obliczyć E{XY).

Zadanie 4. Podany jest fragment wyników testowania pewnej hipotezy dotyczącej zmiennej TIME (dane NEWCOMB2).

(a)    (2 pkt.) Sformułować hipotezę, której dotyczy fragment wydruku.

(b)    (2 pkt.) Jakiego testu użyto i jaki jest wynik testowania hipotezy z punktu a.

(c)    (2 pkt.) Opisać co przedstawiono na rysunku, na którym umieszczono wartość ChiSquare =

81.40.

Zadanie 5. Poniżej zamieszczono fragmenty wydruków dotyczących dopasowania modelu regresji do zmiennej ROOMS (liczba posprzątanych pokoi) w oparciu o liczbę sprzątaczek (NOCREWS).

(a)    (1 pkt.) Podaj procent zmienności liczby posprzątanych pokoi niewyjaśnionej przez zaproponowany model.

(b)    (1 pkt.) Jaki jest typ zależności liniowej?

(c)    (2 pkt.) Sformułuj hipotezę zerową i alternatywną, której odpowiada liczba 305,27. Jaką decyzję podejmiesz w tym przypadku? Uzasadnij.

(d)    (2 pkt.) Dokonaj analizy wartości resztowych.

4