Rzuty mongea131

73

N

b)

OA

Rys. 67

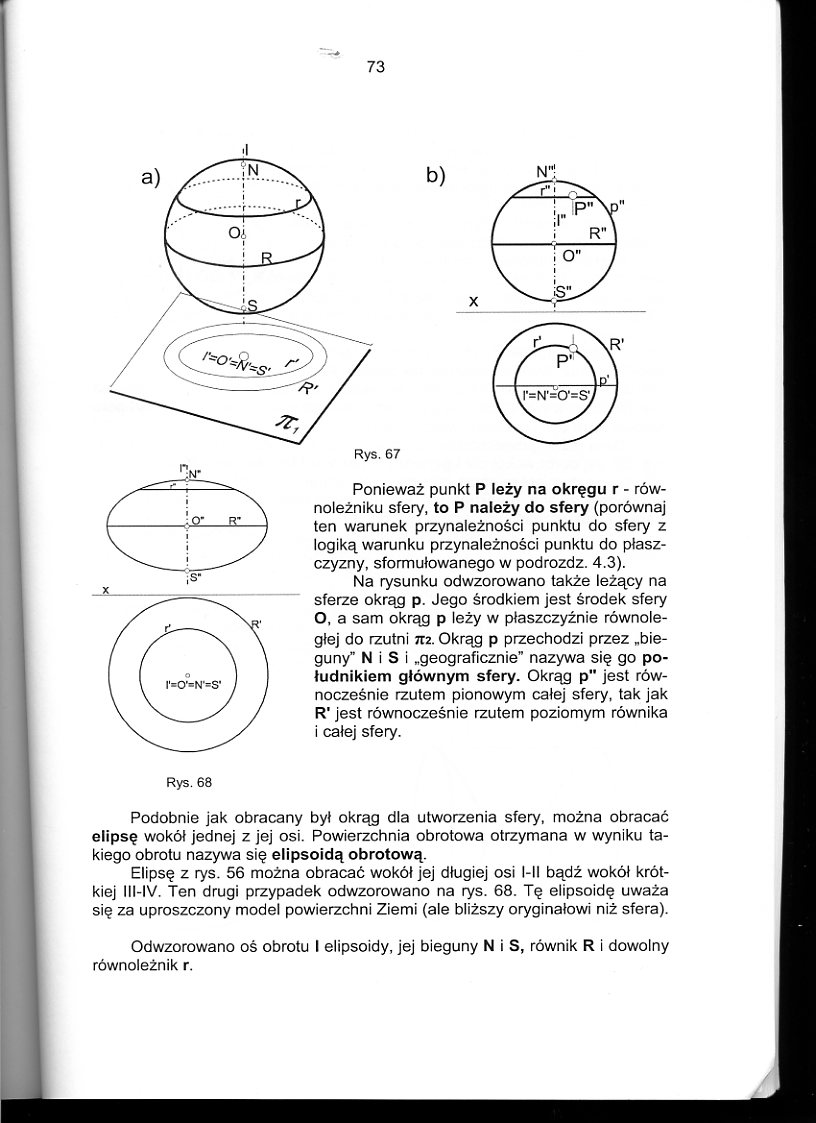
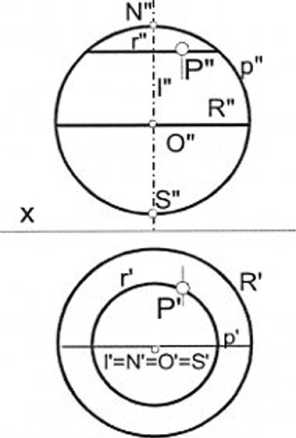
Ponieważ punkt P leży na okręgu r - równoleżniku sfery, to P należy do sfery (porównaj ten warunek przynależności punktu do sfery z logiką warunku przynależności punktu do płaszczyzny, sformułowanego w podrozdz. 4.3).

Na rysunku odwzorowano także leżący na sferze okrąg p. Jego środkiem jest środek sfery O, a sam okrąg p leży w płaszczyźnie równoległej do rzutni 712. Okrąg p przechodzi przez „bieguny” N i S i „geograficznie” nazywa się go południkiem głównym sfery. Okrąg p” jest równocześnie rzutem pionowym całej sfery, tak jak R' jest równocześnie rzutem poziomym równika i całej sfery.

Podobnie jak obracany był okrąg dla utworzenia sfery, można obracać elipsę wokół jednej z jej osi. Powierzchnia obrotowa otrzymana w wyniku takiego obrotu nazywa się elipsoidą obrotową.

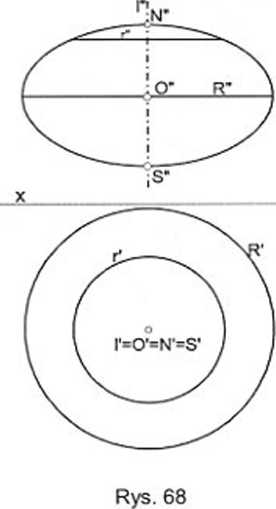
Elipsę z rys. 56 można obracać wokół jej długiej osi I-II bądź wokół krótkiej lll-IV. Ten drugi przypadek odwzorowano na rys. 68. Tę elipsoidę uważa się za uproszczony model powierzchni Ziemi (ale bliższy oryginałowi niż sfera).

Odwzorowano oś obrotu I elipsoidy, jej bieguny N i S, równik R i dowolny równoleżnik r.