Scan0042

Element prętowy na płaszczyźnie

Rozważymy pręt sprężysty o sztywności EA i długości / w lokalnym (tj. związanym z prętem) układzie współrzędnych (x’_Łv’).

u.

Ql

1

-K

EA

q’₂

Z poprzednich rozważań wiadomo, że

\Qu\ ₌ ęa\ i -i

I02xj ~L“ 1 ^]JW

Q' = k'u'

c

- s

W ogólnym przypadku pręt może być nachylony do osi globalnego układu (*,>')• Transformację dowolnego wektora przemieszczenia u z układu globalnego do lokalnego można zapisać:

=> u' = tu, gdzie t =

u' = ucosO + vsin# v' = vcos<9 - ?*sinć9

Element prętowy na płaszczyźnie ma 4 stopnie swobody, więc

							Qu
w	( _	t 0'	^V1	• = Tu => u' = Tu, analogicznie •	Q'\y	• = T<
u'2		0 t	u2		Qix		Qzx
^V2.			^V2.		02,.		02,.

Q' = TQ.

Równanie równowagi MES pręta płaskiego o czterech stopniach swobody, zapisane w

Q\x		' 1	0 -1	0‘	^u'\
Q'\y	_ EA	0	0 0	0
Qix	1	-1	0 1	0	u'2
02,		0	o «—■ o	0	y'i.

macierz sztywności pręta

układzie lokalnym, ma postać:

Drugi i czwarty wiersz i kolumna macierzy sztywności sązerow^re. Macierz sztywności elementu o 4 stopniach swobody musi mieć

© J. Pelc

WMT/84

wymiary 4 x 4 i zawsze jest macierzą symetryczną.

Jeżeli skorzystamy z przekształceń Q' = TQ i u' = Tu, to

Q' = k'u' => TQ = k'Tu => Q = (^rr'kT)i, czyli

Q = ku

k = T^_1kT - macierz sztywności płaskiego elementu prętowego w układzie globalnym

—1 T

(x,y). Należy zaznaczyć, że w przypadku macierzy ortogonalnych jest T = T .

Po wykonaniu naznaczonych mnożeń macierzy otrzymamy ostateczną postać macierzy

sztywności:
	^ui	^V1	»2	v2				^V2
	c^1 2 3 4	CS	-c^2	-CS	U\	y		2,
	CS	s^2	-CS	-s^2	^V1	V			%
/	-c^2	-CS	c^2	CS	^w2	1
	— CS	-s^2	CS	s^2 .	^v2	JL ś	p-—►-^1—		—► X

Przykład 1. Wyznaczanie sil w prętach kratownicy za pomocą MES.

1

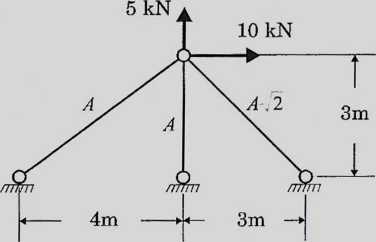
   Dyskretyzacja: numeracja elementów i węzłów

2

   Analiza elementu: budowa macierzy sztywności elementu w postaci pręta kratownicowego

3

   Agregacja: budowa macierzy' sztywności układu (równania równowagi MES)

4

   Wyznaczenie przemieszczeń węzłów': rozwiązanie układu równań