SDC10514

2.5.2. Wzory praktyczne do obliczania drgań bloków na ciągłym sprężystym podłożu

Drgania nietłumione. Rozwiązania podanych poprzednio równań pozwalają wyznaczyć częstości drgań własnych układu oraz amplitudy drgań wymuszonych pod wpływem sił wzbudzających. Wzory do obliczania tych wartości dla układu o dwóch płaszczyznach symetrii i dla harmonicznych sił wzbudzających przytoczono w tabl. 2-8 i 2-9.

Tablica 2-8

Częstości drgań własnych bloku opartego na ciągłym sprężystym podłożu w płaszczyźnie XZ

1. Drgania własne pionowe X

Op

PO,

Równanie drgań własnych pionowych rri2+KiZ ■ 0 lub

Ź?+Ajz rn 0

Prędkość kątowa drgań własnych pionowych

]/•£

r ^m

[2-671

[2-68]

12-69J

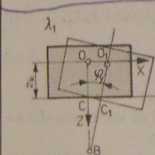
2. Drgania własne złożone (wahadłowe)

li ^1	w
©	IW- jaw
1©	U 2

3. Drgania własne skrętne względem osi pionowej

fc

Równania drgań własnych złożonych

mx+KxX+K_xz_kq)_f — 0;    Q,<p,+K,ZkX+K₉,<p, = 0

Równanie częstości drgań własnych

-K2zi + UC₉,+K_l,zi-e,P)- (K_M-mX²) « 0 lub    0A*-(Aj+AJ,)A² + AjA,, = 0

Prędkość kątowa drgań własnych złożonych

Oznaczenia 0 =

12-701

[2-71]

[2-72J

Aj.a - j/-^- [(A* + AJ,) t |/(AJ + AJ,)*-40 Aj AJ, ]    [2-73]

1

Aj

AT,

m

AJ,

©,+mzj ’    * m    ^f ©,+mzj

— odległość środka ciężkości układu od sprężystego podłoża ©,— moment bezwładności masy układu względem osi Y prostopadłej do płaszczyzny drgań

Równanie drgań własnych skrętnych

+tC₉,q>, = 0

I lub    +    “ 0

Prędkość kątowa drgań własnych skrętnych

[2-74]

[2-74a]

(2-7JJ

©, — moment bezwładności masy układu względem pionowej osi Z

97

7 Fundamenty pod maszyny