SDC10515

Tablica 2-9

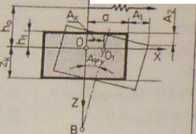
Amplitudy drgań wymuszonych nlethunionych bloku opartego na ciągłym sprężystym podłożu w płaszcz# XZ (por. taM. 2-8)

Tablica 2-9

1. Drgania pionowe (przesuwne)    J

Równanie drgań wymuszonych układu mz + K,z — Po, sina)/ Amplituda drgań wymuszonych

POz    Po,

K,—ma>²    mQ£—co²)

= A₀,v

£2-761 [2-77J,

gdzie:

Ao, ¹

Po.

Jr.

-przemieszczenie układu pod statycznym działaniem

siły P„

W

— współczynnik dynamiczny

rj =--stosunek częstości wzbudzającej do własnej pionowej

Drgania złożone (wahadłowe)

Równania drgań wymuszonych układu

mx+K,x+K,z_kq>, = P₀, sińcu t 8,<p,+K_xz,x+K₉,<p, = M₀,sincot Amplituda drgań wymuszonych środka ciężkości układu (if»,+K_xz}—0,co²) P_0x—K, z, Mof

[2-78)

S.gsincjt

-K,z_tP₀.+ (Kx-moi²)Mo, .

A., --;-1 ^rad

, ni [2-79] [2-1

przy czym

A ■= mQ<a*—(Kę,m+Kxmzl+K,Q)m¹+KxK_v, [2-81]

lub

A — mQ(X\—co²) (2|—co²)    [2-81a]

gdzie:

M₀, = M'o,+Poxho — moment wzbudzający Pox, Mi, — amplitudy składowej poziomej sił wzbudzających i momentu wzbudzającego maszyny

3. Drgania skrętne względem osi pionowej

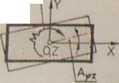
Równanie drgań wymuszonych układu

B,<p,+Kf,<p, = A/o.sineut Amplituda drgań wymuszonych

,    ńdo.    Mo,    _J

” ⁼ e.(^.-m>) |    ⁼ Aoę,v

gdzie:

Mo,

Aoo, ff. —— — skręt układu pod statycznym działaniem momen-*** tu Mo,

v = !■ j-—-y | — współczynnik dynamiczny <u

V *• -j--stosunek częstości wzbudząjącej do własnej skrętnej

dę>s

[2-82]

Uwago, Przy braku składowej siły poziomej do podanych wzorów naleiy podsuwić P₀ ■ 0.

W równaniach ruchu pominięto jako nieznaczny moment statycznego oddziaływania m sprężystego podłoża względem środka ciężkości układu w postaci czynnika mg:_k,<p , I Korzystając z tablic należy pamiętać, że współrzędne wprowadza się z odpowiednimi znakami.

Amplitudę drgań dowolnego punktu układu oblicza się sumując składowe przesunięcia powstałe z przesuwu środka masy układu i z obrotu układu, np. pozioma amplituda drgań krawędzi górnej powierzchni bloku wynosi

'łi* ⁼    [2-83]

pionowa zaś [2-84]

Wartości pomocnicze A_x = ~y i A^ = y    mają sens fizyczny jako gra

niczne prędkości drgań własnych układu, które występowałyby w następujących przypadkach:

A_x — przy sztywności podłoża K_v rosnącej nieograniczenie, tj. przy -* oo,

Ay — przy sztywności podłoża K_x rosnącej nieograniczenie, tj. przy K_x -* oo.

Zawsze zachodzi następująca zależność między prędkościami drgań własnych złożonych Aj i A2 oraz prędkościami granicznymi A_x i A,:

At < A_x < A₂

oraz

Aj < Ay < Aj.

P-85]

Posługując się prędkościami granicznymi A_x i A, można obliczyć prędkości drgań złożonych Aj i Aj z zależności podanej przez Barkana [3]

[2-86]

^f.2 —

Współczynniki /?j i fi₂ należy przyjmować z wykresu (rys. 2-18) w zależności od war-A²

tości stosunku -A- oraz wartości & (por. tabl. 2-8 — wzór [2-73D-

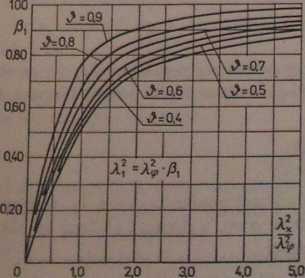
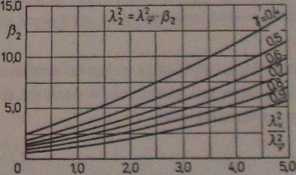
Rys. 2-18. Wykres współczynników fi, i fi, do wyznaczania częstości drgań złożonych