skanowanie0078

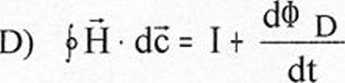
89. Gęstość stanów g(p) w przestrzeni pędów możemy zapisać:

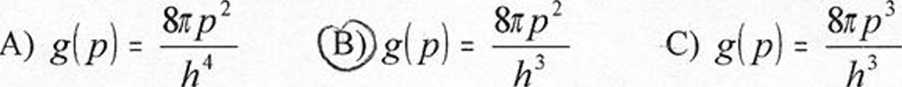
gdzie p to pęd mikrocząstki, a h to stała Plancka.

90.    W zależności od stopnia uporządkowania struktury wewnętrznej ciała stałe (czyli ciała odznaczające się stabilnością kształtu) dzielimy na ciała krystaliczne i amorficzne. Ciała krystaliczne są to ciała które:

A) wykazują okresowe uporządkowanie tylko wewnątrz pewnych obszarów zwanych ziarnami krystalicznymi,

(Bjwykazują okresowe uporządkowanie (atomów jonów lub cząsteczek) dalekiego zasięgu w przestrzeni

C)    wykazują jednakowy rozkład radialny (atomów jonów lub cząsteczek) we wszystkich kierunkach.

D)    wykazują uporządkowanie krótkiego zasięgu w całej objętości kryształu

91.    Szerokość poziomu energetycznego elektronu walencyjnego AE w krysztale jest w przybliżeniu równa

A) A E = 100 eV B)AE= 1000eV 0)AE=leV D)AE=10eV

92.    Wzór na siłę Lorentza ma postać i opisuje:

A)

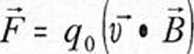
Zależność siły F od prędkości V przewodnika poruszającego się w polu magnetycznym o indukcji R

F=    ^xB) Zależność prędkości D ładunku próbnego q₀ poruszającego się w polu

magnetycznym o indukcji R od sity F działającej na to pole

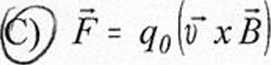
F - q₀\v xBj Zależność siły F od prędkości \F ładunku próbnego q₀ poruszającego się w polu elektrycznym o indukcji R

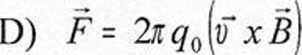
F - 2Kqą\o xB) Zależność siły F od prędkości U ładunku próbnego q₀ poruszającego się

w polu magnetycznym o indukcji R

93. Znając energię elektronu E_Fna poziomie Fermiego możemy policzyć prędkość elektronu V_F na poziomie Fermiego czyli tzw. prędkość Fermiego. Prędkość Fermiego wyraża się wzorem:

94. Steradian jest to jednostka miary:

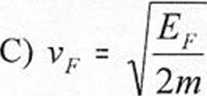
A) kąta płaskiego zawartego między dwoma promieniami koła, wycinającymi z jego okręgu łuk o długości równej obwodowi tego koła,

B) , kąta bryłowego o wierzchołku w środku kuli, wycinającym z jej powierzchni część równą powierzchni kwadratu o boku równym połowie promienia tej kuli,

C) łukowej kąta płaskiego, równa stosunkowi promienia kuli r do powierzchni S wyciętej przez ten kąt,

(0} kąta bryłowego o wierzchołku w środku kuli, wycinającym z jej powierzchni część

równą powierzchni kwadratu o boku równym promieniu tej kuli, (^ - —).

r