skanuj0003 [Rozdzielczość Pulpitu]

2. y.u:.i<r..i,u-I. ■ • i.............    1 •:» i    : .•    . i

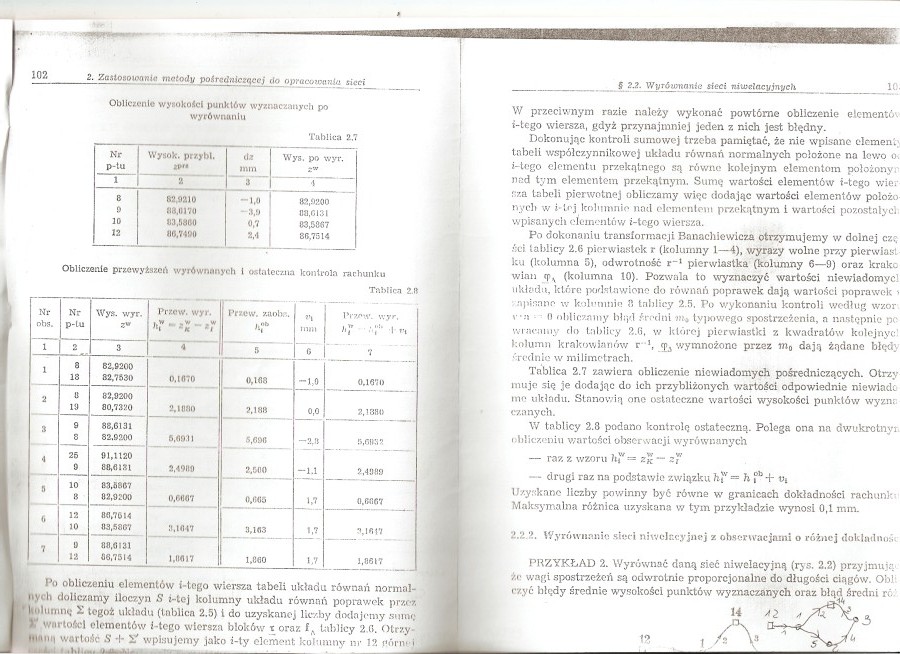
Obliczenie wynokoicl punktów wyznaczanych po wyrównaniu

Tablica 2.7

Po obliczeniu elementów i-tego wiersza tabeli układu równań normalnych doliczamy iloczyn S i-tej kolumny układu równnń poprawek przez Ikolunme I tegoż układu (tnbllcn 2.5) l do uzyskanej liczby dodajemy smm; fł Wartości elementów i-tego wiersza bloków t oraz f_A tablicy 2.0. Otrzy-IW*mi wartość S + wpisujemy jako i-ty element kolumny nr 12 i-Orm i^

W przeciwnym razie należy wykonać powtórne obliczenie elcmentó i-tcgo wiersza, gdyż przynajmniej jeden z nich jest błędny.

Dokonując kontroli sumowcj trzeba pamiętać, że nie wpisane elemen. tabeli współczynnikowej układu równań normalnych położone na lewo o. i-tego elementu przekątnego są równe kolejnym elementom położony nad tym elementom przekątnym. Sumę wartości elementów i-tcgo wie * r:za tabeli pierwotnej obliczamy więc dodając wartości elementów polożo nycli w »• lej kolumnie nad elementom przekątnym i wartości pozostałych wpisanych elementów i-tcgo wiersza.

Po dokonaniu trunslormacji Banachiewicza otrzymujemy w dolnej cz; ści lablicy 2.6 pierwiastek r (kolumny 1—4), wyrazy wolne przy pierwiast ku (kolumna 5), odwrotność r~‘ pierwiastka (kolumny 6—9) oraz krakc wian q\ (kolumna 10). Pozwala to wyznaczyć wartości niewiadomyc! układu, które podstawione do równań poprawek dają wartości poprawek ' opinane w kolumnie 0 lablicy 2.5. Po wykonaniu kontroli według wzór v:» n obliczamy bb}d średni tyjiowego spostrzeżenia, n następnie pc wrncimiy tlo tablicy 2.6, w której pierwiastki z kwadratów kolejnye! l-.olumn krakowianów r \ wymnożone przez m₀ dają żądane błędy •Tfdnłe w milimetrach.

Tablica 2.7 zawiera obliczenie niewiadomych pośredniczących. Otrzymuje się je dodając do ich przybliżonych wartości odpowiednie niewiadc me układu. Stanowią ono ostateczno wartości wysokości punktów wyzn; czanych.

W tablicy 2.8 podano kontrolę ostateczną. Polega ona na dwukrotny* i bliczcniu wartości obserwacji wyrównanych

— drugi raz na podstawie związku h? = h ?^b + u,

Wzyskane liczby powinny być równe w- granicach dokładności rachunl-Maksymalna różnica uzyskana w tym przykładzie wynosi 0,1 mm.

2.2,2. Wyrównanie sieci niwelacyjnej z obserwacjami o różnej dokładno:,

PRZYKŁAD 2. Wyrównać daną sieć niwelacyjną (rys. 2.2) przyjmuj?, że wagi spostrzeżeń są odwrotnie proporcjonalne do długości ciągów. Obi rzyć błędy średnie wysokości punktów wyznaczanych oraz błąd średni rć.