skanuj0006 [Rozdzielczość Pulpitu]

jąccj mu obserwacji. Zrównoważone równania poprawek zajmują dolną linię każdego wiersza.

< Układ zrównoważony posłużył do zestawienia równań normalnych (tablica 2,14). Hnchunck skontrolowano kolumnami sumowymi S i Element i-ty kolumny S jest iloczynem i-tej kolumny krakuwianu wkjhjI-czynnikowcgo zrównoważonemu układu równań poprawek, przez ich kolumnę S. Uzyakujo «lq go, oczywiście, na podstawie danych tablicy 2.12. Element i-ty kolumny £ tablicy 2.14 jest sumą wartości elementów i-Lega wiersza tabeli uklndll równań normalnych. Uzyskane liczby powinny być identyczne w granicach dokładności rachunku.

Rozwiązanie układu przeprowadzono metodą nieoznaczoną. Obliczenie kofaktorów skontrolowana mnożąc i-tą kolumnę tabeli współczynnikowej układu równań normalnych przez i-tą kolumnę tabeli kofaktorów. Uzyskane wartości wyznaczniku podstawowego układu równań normalnych wpisano pod tabelą (A*) '.

Niewiadome układu podstawiono do zrównoważonego okładu • ’>v, poprawek (tablica 2.1.3) otrzymując poprawki zrównoważone Pi r..-|jv Wpisano je w dolnej linii każdego wiersza w ostatniej kolumnie. Poprawki obserwacyjne tą obliczono dzieląc poprawki zrównoważone przez pierwiastki z odpowiadających tm wag, Din kontroli wykonano rachunek powtórnie, podstawiając niewiadomi' układu do niezrównoważonych równań poprawek.

Poniżej tablicy 2.13 podano wyniki kontroli VA 0 oraz W > l,V. Jak widać opiera się ona nn poprawkach zrównoważonych i tabeli zrównoważonego układu równań błędów. Znajduje się tam również wartość błędu średniego m_c typowego fipoatr/eżniln, którą obliczono wykorzystując znaną sumę kwadratów poprawek zrównoważonych.

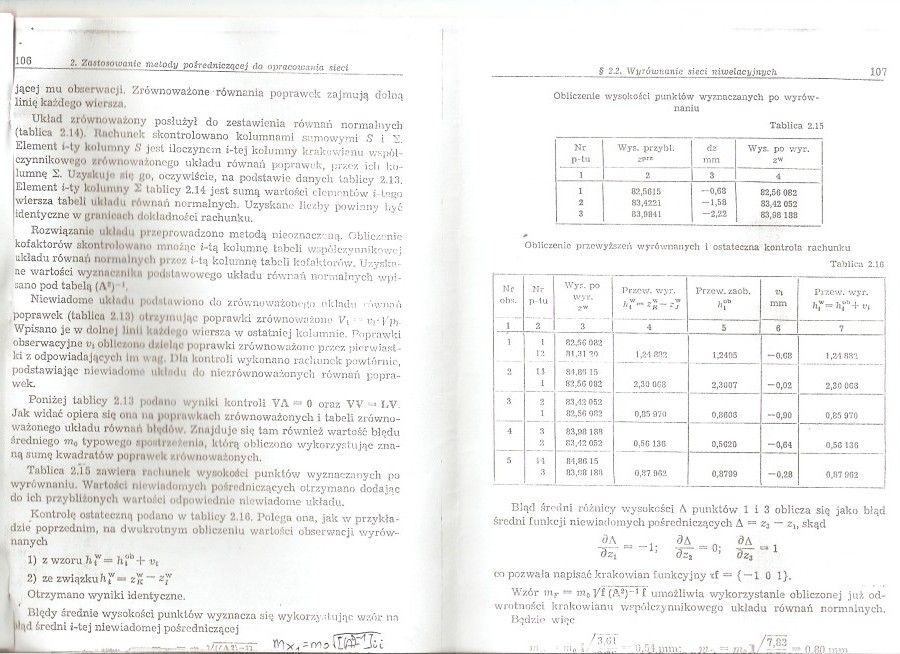
Tablica 2.15 zawiera rachunek wywokoścl punktów wyznaczanych pu wyrównaniu. Wartości niewiadomych pośredniczących otrzymano dodając do ich przybliżonych wartości odpowiednie niewiadome ukłatiu.

Kontrolę ostateczną podano w tablicy 2.18. Polega ona, jak w przykładzie poprzednim, na dwukrotnym obliczeniu wartości obserwacji wyrównanych

1)    z wzoru h? =■ h|^b-ł- V|

2)    ze związku hj* “    ~ ^z7

i Otrzymano wyniki identyczne.

*1 Błędy średnie wysokości punktów wyznacza się wykorzy.dująć wzór na błąd średni i-tej niewiadomej pośredniczącej    .

J    .    ,/77>r:-,r

Obliczenie wysokości punktów wyznaczanych po wyrów-Tablica 2.1S

Obliczenie przewyższeń wyrównanych i ostateczna kontrola rachunku

Błąd średni różnicy wysokości A punktów 1 i 3 oblicza się jako błąd średni funkcji niewiadomych pośredniczących A = z₃ — z_u skąd dA _ AA

Si; ~ '■ sr,-°' zę ¹

co pozwala napisać krakowian funkcyjny tf =* { — 1 0 1}.

Wzór in_r — jn₀Vf (A*)^-1 f umożliwia wykorzystanie obliczonej już odwrotności krakowiana współczynnikowego układu równań normnlnych.

Będzie? więc