skanuj0007 [Rozdzielczość Pulpitu]

3	2. Zasfojoauuie metody poireduicręeej do op

i I^-1l	13,01	1,79	0,56 j
°	1,79	7,83	2,44
	|0,56	2,44	3,76]
(-3,05!	1 l~‘l
i °'^65'	^0	» 0,721
[ 3,20	II l|
,«m,VQlL’ o;		71 mm

2.3. Wyrównanie sieci liniowych

PRZYKŁAD. Wyrównać daną sieć trilateracyjną (rys. 2.3) ora/, ubliżyć:

1)    błędy średnie współrzędnych punktów 2 i 3

2)    błąd średni długości dj. ₃

3)    błąd średni azymutu <pi. a

4)    błąd średni kąta a u, *, ₃.

Dane uwierają tablice 2.17 i 2.18. Rozwiązanie — tablice 2.19 do 2.24.

310*1,80

7486,92

8875,64

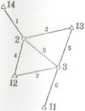
Rys. 2.3

Nr I Wart. observ

2510,63

7020,01

1002,65

Obliczenie współrzędnych punktu nr 3 wcięciem liniowym z punktów 11 i 12

3.617,04

3.626,16    3.801,37

1025,43    5468,76 I 3106.89    2510,63 !

-23,43732 14,38436 j 23.43732 11,78160 | 26,10596

~ 4 612,28; y, - 6 001.22

r 2 wcięciom liniowym z punk-3.801,37

Obliczenie współrzędnych z. punktu tów 3 i 12

3.535,53    3.458.95

4612,28    CDU 1,22 , 3106,89    2510,63

-22,31451 13,91478 | 22,31451 14,98605 28,90083

*,= 6 526,79    ; y» - 3 028,91

Rachunek rozpoczynamy obliczeniem przybliżonych współrzędnych punktów nr 2 i 3. Stosujemy wcięcie liniowe wykorzystując zaobserwowane długości boków.

Tablica 2.19 zawiera obliczenie przyrostów przybliżonych współrzędnych. współczynnik! cos t|>, sin <f- i wyrazy wolne (w centymetrach).

Równania poprawek w postaci tabelarycznej zestawiono w tablicy 2.20.

W tablicy 2.21 wpisano równania poprawek w postaci algebraiczne; oraz zrównoważono układ dzieląc współczynniki i wyraz wolny każdego równania przez błąd średni odpowiedniej obserwacji. Równania zrównoważone wpisano w dolnej linii każdego wiersza. Tabelę uzupełniono kolumną sumową.

Tablica 2.22 zawiera w bloku górnym:

—    równania normalne, zestawione na podstawie zrównoważonego układu równań poprawek.

—    krakowian jednostkowy,

i przyrost

—    krakowiany funkcyjne f_rt, f,.,

Krakowian funkcyjny f.« zestawiono korzystając z

różniczkowy długości boku d*j

1 dx₃

dyj

duli -

| dx, dy,

J