skanuj0001 [Rozdzielczość Pulpitu]

98_2. Zastosowanie metody pośredniczącej do opracowania sieci__

cji wyrównanych, gdyż żądane wartości współrzędnych daje rachunek niewiadomych pośredniczących.

W zależności od rodzaju obserwacji rozróżniamy sieci płaskie kątowe, kierunkowe, ozymutalne, liniowe, kąlowo-liniowe, azymutalno-liniowc itd.

Pewne typy płaskich sieci geodezyjnych mają swe ustalone nawy określające kształt elementów geometrycznych, z których są zbudowane oraz rodzaj wykonanych obserwacji.

Sieć triangulacyjna jest zbudowana z trójkątów, których wierzchołkami są jej punkty. Obeserwuje się kąty trójkątów. Jest to więc sieć kątowo. Pomiar długości niewielkiej liczby boków sieci (tzw. baz) nie powoduje zmiany jej nazwy. Dla sieci triangulacyjnych z pomiarami bazowymi pozostawiono tą samą nazwą, chociaż są to sieci kąlowo-liniowe.

Sieć trilhteracyjna jest również zbudowana z trójkątów, których wierzchołkami są jej punkty. Obserwuje sią długości boków trójkątów. Jest to więc sieć liniowa.

Sieć poligonowa jest siecią geodezyjną złożoną z powiązanych z sobą linii łamanych, których wierzchołkami są punkty sieci. Pomiarowi podlegają kąty wierzchołkowe oraz długości boków poligonu (bolcami poligonu nazywa sią poszczególne odcinki linii łamanej). Sieci poligonowe są więc sieciami kątowo-Iiniowymi.

Istnieje możliwość konstruowania sieci złożonych z kilku wymienionych wyżej typów.

§ 2.2. Wyrównanie sieci niwelacyjnych

2.2.1 Wyrównanie sieci niwelacyjnej z obserwacjami jednakowo dokładnymi

PRZYKŁAD 1. Wyrównać daną sieć niwelacyjną (rys. 2.1) przyjmując obserwacje za jednakowo dokładne. Obliczyć błędy średnie wysokości punktów wyznaczanych oraz błąd średni różnicy wysokości A punktów 8112.

19

25

____§ 2.2. Wyrównania giccj niwelacyjnych___99

Na rysunku strzałkami zaznaczono kierunki wzniesień. Dane zawierają tablice 2.1 i 2.2.

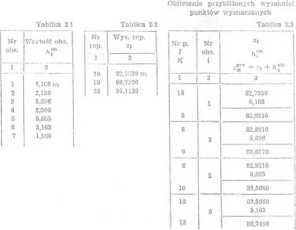
Rachunek rozpoczynamy od obliczenia przybliżonych wartości niewiadomych pośredniczących, którymi są wysokości punktów wyznaczanych. Wykorzystujemy do logo znane wysokości reperów oraz przewyższenia zaobserwowane. Tak np. przybliżoną wartość wysokości punktu nr 8 otrzymujemy jako sumą wysokości reperu nr 18 i przewyższenia nr 1. Podobnie wysokość przybliżoną punktu nr 9 obliczamy jako sumą otrzymanej uprzednio wysokości punktu nr 8 i obserwacji nr 3. Rachunek zawiera tablica 2.3.

W tablicy nr 2.4 obliczono przybliżone wartości przewyższeń jako róż

nice przybliżonych wysokości punktów K (wyższego) oraz I (niższego) każdego ciągu. Różnice h_t^prz — fi,^6b I*, dają wyrazy wolne równań poprawek.

Równania poprawek zapisano w tablicy 2.5, przy czym za punkt K (końcowy) przyjmowano konsekwentnie wyższy z dwóch punktów knż.i- _:: • ciągu Wykorzystano Ul wzór nn równanie pcę>r ivld pr-.-.    ' .    i.:.v-U®*>