skanuj0004zv

7.Korzystając z definicji obliczyć rząd macierzy

	1 2 v 1 1		1 -1 2'
aj .4 =	2 4 2 0 5 10 -1 3	Odp: r(A)=2 b) A =	-1 1 -2 2-2 4	Odp: r(A)=l

a\A =

8.Znależć rząd macierzy sprowadzając macierz do postaci bazowej

			1	1	1	1 '		1 -1	0 2	3'
"1 -1	2 -||		2	2	3	-1		I^1 2	1 0	2
0 2	-2 4	b) B =	0	0	1	-3	ę) C =	0 1	1 2	5
2 0	3 3
			3	3	5	-2		^1 0	1 4	8

Odp: r(B)=3 ;

Odp:rfCH2.

ą)

Odp: r(A)=3;

9.Metodą przekształceń elementarnych rozwiązać układ równań liniowych

z, + z2 + z3 = —1	z, =i(l-2f)	2xl +x2+x3 =2
2z.-z,+z, =2	1	x, +3x? +jc, -5 m
] ’ ^2 CM Qto\	x2=--(4+0; bi	^1 2 3 Odp: \
5z, —x2 + ix3 =3		z, + z2 + 5z3 -7
7z, - 2z2 + 4x3 = 5	x3=t	2z, +3z2 -3z3 = 14

x₂ = 2 ;

I x, = -2

ci

z,-x₂ + 3x₃ —x_t = -2 2x, +3x₂ +x₃ +x₄ = 0 4x, + 3x₃ - 2x„ = -1 3x, + 2x, + 5x, + 2x, = 3

Odp:

|3z, - 2x₂ + 5x₃ + 4z₄ — 2 5z, - 4x₂ + 4z₃ + 3x₄ = 3 Odp: 3z, - 6z₂ + 3z₃ + 2x₄ = 4

Iz, +x₂ +z₃ = 2 2x, -3z₂ + 4z₃ = 3 Odp: <j 4z, — 1 lz₂ +10z₃ = 5

(2x, — z₂ +x₃ +2x_t = 3 z, +z₂ -2x₃ + 2z₄ = 2 Odp: 3x₂ — 5z₃ +2z₄ =1

z, =2 x₂ =-2

z₃=-l’

x. =3

di

z₃ = 6-15f+10s r₄ =-7 + 18/-12z z, =1/5(9-70 x₂ = 1/5(1 + 2f)    h) •

x₃ =/

z, = |(5-/-2s) z₂=i(l+5r-2s);

Z,=tAZ,=S

z, +z₂ -3z₃ -•-!

2z, +z₂ +x₃ =1 z, + Z2 + z₃ =3 z, +2z₂-3z₃ =1

t, -2z₂ +4z₃ = 0 x,+x₂+XjH0 Odp: z, -Z,!«tO

Odp: sprzeczny;

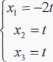
z, +2x₂ -z₃-z₄ =1

z, +x₂ +Zj +3z₄ = 2 Odp:sprzeczny;

3z, +5z, -z, +z₄ =3

10* .Przedyskutować rozwiązywałność układu równań w zależności od parametru ae 1<.

Iax_l-x₂+x₃ =1 z, - ax₂ + z₃ = 1 3z, — 3z, + 2x₃ = 2 a

Iz, + 2x₂ + 3z₃ = 0 2z, +4z₂ +2 ax₃ = 0 z, + 3z, +x, = a—3

6