skanuj0038 3

^o( li wykresów ilustrujących prawidłowość, zgodnie /. którą wraz ze zrostem stopnia zbrojenia maleją naprężenia w stali rozciąganej i w hemie (rys. 6.20, 6.21).

6.9. Podsumowanie

Przedstawiony wyżej nieliniowy model obliczeniowy przekroju w ujęciu mi hi notorycznym opisuje w sposób kompleksowy zachowanie betonu ulali w całym zakresie deformacji, począwszy od fazy sprężystej aż do lo/.liwych faz uplastycznienia materiałów. Jego podstawową zaletą jest inżliwość wyznaczenia odkształceń i naprężeń w przekroju pod działalno sil przekrojowych N, M, wywołanych obciążeniem obliczeniowym, o/.wiązanie problemu wymaga zastosowania niestandardowych metod ptymalizacji. Podejście to pozwoliło na przeprowadzenie analiz parame-yrznych, umożliwiających zbadanie wpływu różnych parametrów geoid rycznych i fizycznych na odkształcenia i naprężenia w przekroju. 1 stosunku do propozycji innych autorów, np. Pinfolda [122], Ciesiel-l icgo [21], Bachmanna [1], Niesera i Engela [115], opracowany model i cli uje się większą ogólnością z uwagi na uwzględnienie wszystkich mo-iwyeli w sensie kombinatorycznym postaci rozkładu naprężeń w przemili i wpływu dodatkowego zbrojenia przy otworach oraz dokładniejsze Iw (imwanie cech geometrycznych przekroju.

7. NOŚNOŚĆ I WYMIAROWANIE PRZEKROJÓW ŻELBETOWYCH Z UWZGLĘDNIENIEM FIZYCZNEJ NIELINIOWOŚCI MATERIAŁÓW

7.1. Wprowadzenie

Nośność przekroju żelbetowego mimośrodowo ściskanego określają wartości osiowej siły podłużnej i momentu zginającego, wywołujące gra niczne odkształcenia betonu lub stali zbrojeniowej. Ponieważ oddziaływań siły i momentu nie można rozdzielić ani superponować, nośność przekroju ze względu na siłę zależy od momentu i odwrotnie - na noś ność ze względu na moment zginający wpływa wartość siły, co wykazali m.in. Czkwianianc i Kamińska [29].

W rozdziale 6 przedstawiono algorytm wyznaczania naprężeń w prze kroju pierścieniowym zamkniętym lub osłabionym otworami pod działaniem sił przekrojowych N, M, wywołanych obciążeniem obliczeniowym. W niniejszym rozdziale zostaną określone warunki stanu granicznego nośności przekroju żelbetowego pierścieniowego z uwzględnieniem osia bienia otworami.

7.2. Równania przekroju w stanie granicznym nośności

7.2.1. Przypadek, występowania odkształceń różnych znaków

Rozpatrzymy przypadek wystąpienia w przekroju elementu żelbetowe go granicznych wartości odkształceń e_cu (skrócenie) lub e_su (wydłużenie). Rozwiązanie problemu sprowadza się do znalezienia granicznych warto ści osiowej siły podłużnej N_u i momentu zginającego M_u. Równanie ró wnowagi sił podłużnych w przekroju w stanie granicznym nośności otr/y mujemy, zapisując wyprowadzone w rozdziale 6 równania (6.9) i (6.10) w następującej postaci (przypadek sprężysto-plastyczny - schemat 8):

1 - ą ,    ,

-——(a_b - a,) +

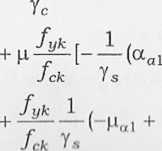
i—^e'_a pćj(a, aj+ 0,25 e'_B X₂(a, a_b)] + Yc

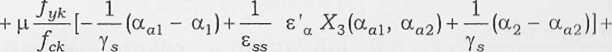
(“Mai + Ma₂) + ™_u = 0,

(7.1)

75