skanuj0060 (Kopiowanie)

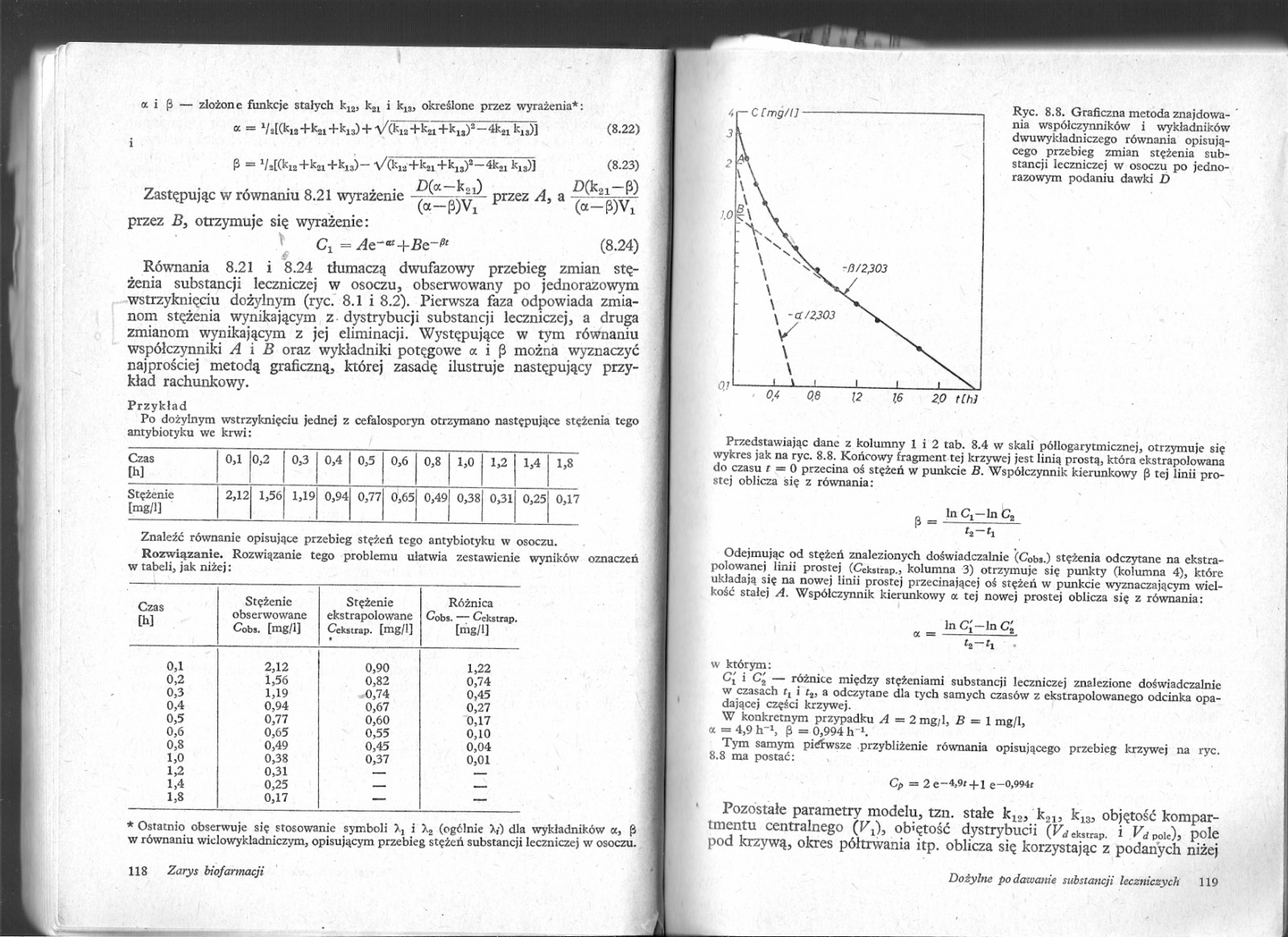
a i {3 — złożone funkcje stałych k₁₂, k_2l i k₁₃, określone przez wyrażenia*:

« = ¹/.[(k»+k₂i+ki₃) + V'(ki_a+fc_łi+k_ł,)^J-4k,₁ k_xł)]    (8.22)

P = Vs((ki2+k_8x +k₁₃)— V(k7a+k,i +k_ls)^J—4k_sl k_ls)j    (8.23)

Ofei-P)

(«-WV_x

przez A, a

Zastępując w równaniu 8.21 wyrażenie przez B, otrzymuje się wyrażenie:

D(a—koj)

^=mr

C_x =Ae-’‘+Be-»‘    (8.24)

Równania 8.21 i 8.24 tłumaczą dwufazowy przebieg zmian stężenia substancji leczniczej w osoczu, obserwowany po jednorazowym wstrzyknięciu dożylnym (ryc. 8.1 i 8.2). Pierwsza faza odpowiada zmianom stężenia wynikającym z dystrybucji substancji leczniczej, a druga zmianom wynikającym z jej eliminacji. Występujące w tym równaniu współczynniki A i B oraz wykładniki potęgowe a i P można wyznaczyć najprościej metodą graficzną, której zasadę ilustruje następujący przykład rachunkowy.

Przykład

Po dożylnym wstrzyknięciu jednej z cefalosporyn otrzymano następujące stężenia tego antybiotyku we krwi:

Czas [h]	0,1	0,2	0,3	0,4	0,5	0,6	0,8	1,0	1,2	1,4	1,8
Stężenie [mg/1]	2,12	1,56	1,19	0,94	0,77	0,65	0,49| 0,38 1		0,31	0,25	0,17

Znaleźć równanie opisujące przebieg stężeń tego antybiotyku w osoczu.

Rozwiązanie. Rozwiązanie tego problemu ułatwia zestawienie wyników oznaczeń w tabeli, jak niżej:

Czas [h]	Stężenie obserwowane Cobs. [mg/1]	Stężenie ekstrapolowane Ceksirap. [mg/1] •	Różnica Cobs. ““ Cekstrap. [mg/lj
0,1	2,12	0,90	1,22
0,2	1,56	0,82	0,74
0,3	1,19	0,74	0,45
0,4	0,94	0,67	0,27
0,5	0,77	0,60	0,17
0,6	0,65	0,55	0,10
0,8	0,49	0,45	0,04
1,0	0,38	0,37	0,01
1,2	0,31	—	—
1,4	0,25	—	—
1,8	0,17	—	—

* Ostatnio obserwuje się stosowanie symboli X, i X₂ (ogólnie X,) dla wykładników a, p w równaniu wiclowykladniczym, opisującym przebieg stężeń substancji leczniczej w osoczu.

118 Zarys biofarmacji

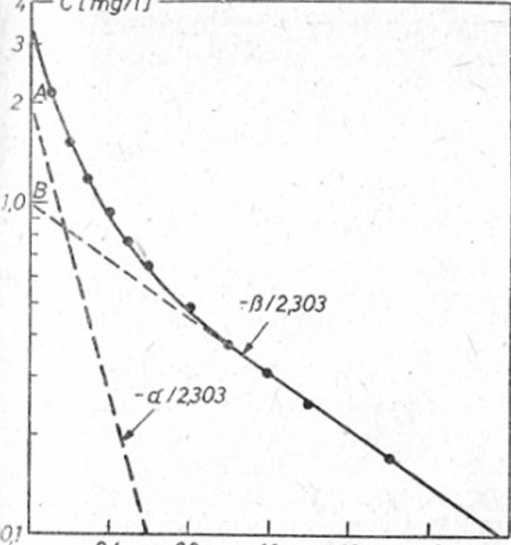
Ryc. 8.8. Graficzna metoda znajdowania współczynników i wykładników dwu wykładniczego równania opisującego przebieg zmian stężenia substancji leczniczej w osoczu po jednorazowym podaniu dawki D

',_rCCmg/f J

0.4    0.6    \2    16 2p t[h]

Przedstawiając dane z kolumny 1 i 2 tab. 8.4 w skali półlogarytmicznej, otrzymuje się wykres jak na ryc. 8.8. Końcowy fragment tej krzywej jest linią prostą, która ckstrapolowana do czasu t — 0 przecina oś stężeń w punkcie B. Współczynnik kierunkowy p tej linii prostej oblicza się z równania:

ln Cj —ln C₂

Odejmując od stężeń znalezionych doświadczalnie (Cobs.) stężenia odczytane na ekstra-

polowanej linii prostej (Cckstrap., kolumna 3) otrzymuje się punkty (kolumna 4), które układają się na nowej linii prostej przecinającej oś stężeń w punkcie wyznaczającym wielkość stałej A. Współczynnik kierunkowy a tej nowej prostej oblicza się z równania:

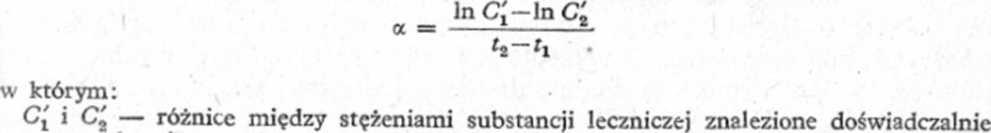
w czasach e_Ł i a odczytane dla tych samych czasów z ekstrapolowanego odcinka opadającej części krzywej.

W konkretnym przypadku A —2 mg/1, B = 1 mg/1, a - 4,9 h^-x, P = 0,994 h'^ł.

Tym samym pićirwsze przybliżenie równania opisującego przebieg krzywej na ryc. 8.8 ma postać:

Cp = 2e-4,9f + l e-0,994r

Pozostałe parametry modelu, tzn. stałe k,,,, k₂₁, k₁₃, objętość kompar-trnentu centralnego (P_Ł), objętość dystrybudi (Pf_Ckstrap. i Vj _poic), pole pod krzywą, okres półtrwania itp. oblicza się korzystając z podanych niżej

Dożylne podawanie substancji leczniczych 119