skanuj0069 (Kopiowanie)

Zarówno r_m,jak i Cmai«. zależą w prosty sposób od stałych ki i K oraz od ułamka wchłoniętej dawki D.

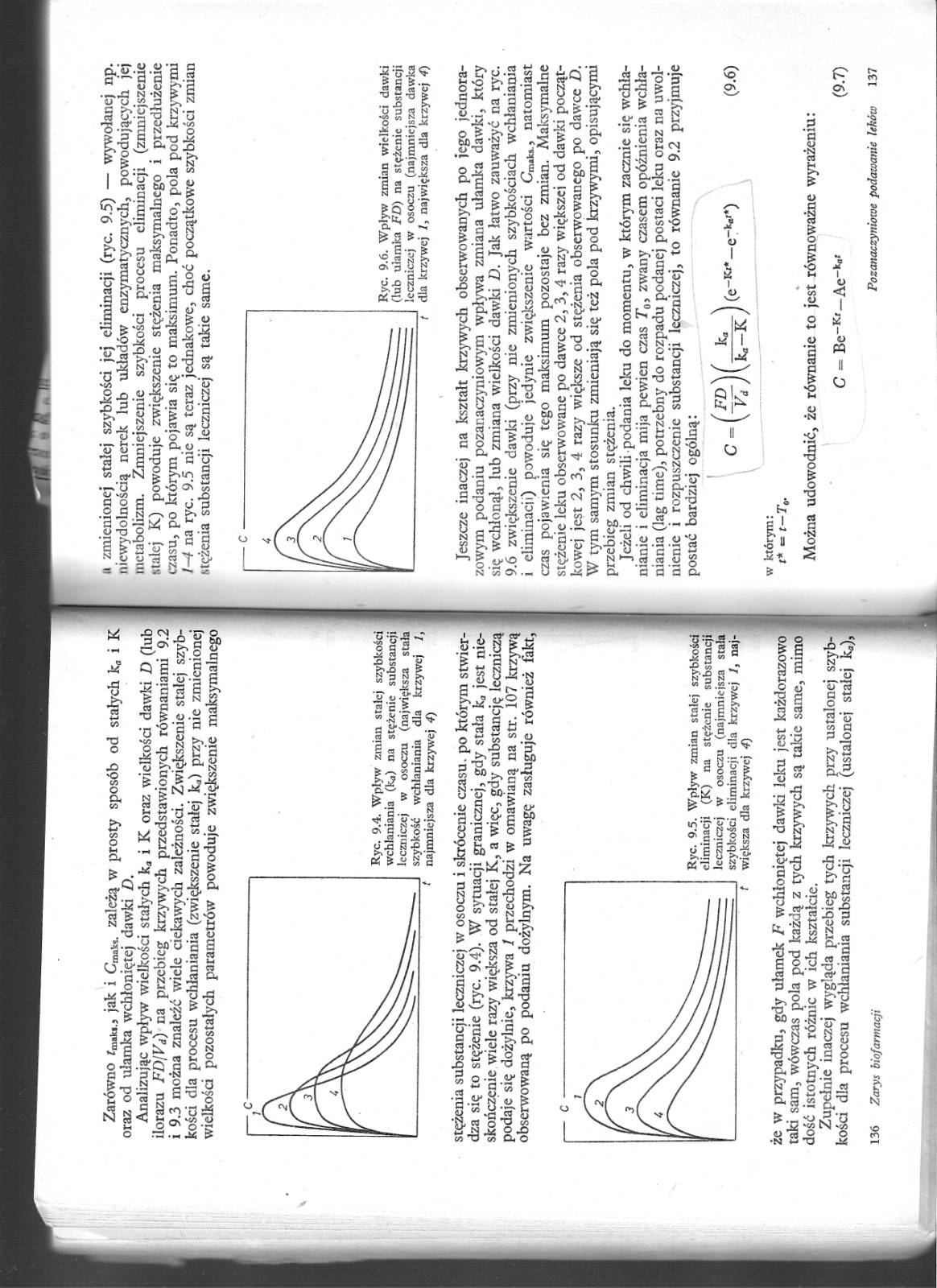
Analizując wpływ wielkości stałych k, i K oraz wielkości dawki D (lub ilorazu FD/Vj) na przebieg krzywych przedstawionych równaniami 9.2 i 9.3 można znaleźć wiele ciekawych zależności. Zwiększenie stałej szybkości dla procesu wchłaniania (zwiększenie stałej k.) przy nie zmienionej wielkości pozostałych parametrów powoduje zwiększenie maksymalnego

stężenia substancji leczniczej w osoczu i skrócenie czasu, po którym stwierdza się to stężenie (ryc. 9.4). W sytuacji granicznej, gdy stała k„ jest nieskończenie wiele razy większa od stałej K, a więc, gdy substancję leczniczą podaje się dożylnie, krzywa 1 przechodzi w omawianą na str. 107 krzywą obserwowaną po podaniu dożylnym. Na uwagę zasługuje również fakt,

że w przypadku, gdy ułamek F wchłoniętej dawki leku jest każdorazowo takt sam, wówczas pola pod każdą z tych krzywych są takie same, mimo dość istotnych różnic w ich kształcie.

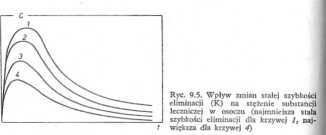
Zupełnie inaczej wygląda przebieg tych krzywych przy ustalonej szybkości dla procesu wchłaniania substancji leczniczej (ustalonej stałej k„), 136 Zarys biofarmacji ■ zmienionej stałej szybkości jej eliminacji (ryc. 9.5) — wywołanej np. niewydolnością nerek lub układów enzymatycznych, powodujących jej metabolizm. Zmniejszenie szybkości procesu eliminacji (zmniejszenie stałej K) powoduje zwiększenie stężenia maksymalnego i przedłużenie czasu, po którym pojawia się to maksimum. Ponadto, pola pod krzywymi 1-4 na ryc. 9.5 nie są teraz jednakowe, choć początkowe szybkości zmian stężenia substancji leczniczej są takie same.

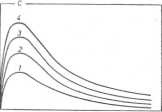
Ryc. 9.6. Wpływ zmian wielkości dawki (lub ułamka FD) na stężenie substancji leczniczej w osoczu (najmniejsza dawka dla krzywej 1, największa dla krzywej 4)

Jeszcze inaczej na kształt krzywych obserwowanych po jego jednorazowym podaniu pozanaczyniowym wpływa zmiana ułamka dawki, który się wchłonął, lub zmiana wielkości dawki D. Jak łatwo zauważyć na ryc. 9.6 zwiększenie dawki (przy nic zmienionych szybkościach wchłaniania i eliminacji) powoduje jedynie zwiększenie wartości Cmak*., natomiast czas pojawienia się tego maksimum pozostaje bez zmian. Maksymalne stężenie leku obserwowane po dawce 2, 3,4 razy większej od dawki początkowej jest 2, 3, 4 razy większe od stężenia obserwowanego po dawce D. W tym samym stosunku zmieniają się też pola pod krzywymi, opisującymi przebieg zmian stężenia.

Jeżeli od chwili podania leku do momentu, w którym zacznie się wchłanianie i eliminacja mija pewien czas T₀, zwany czasem opóźnienia wchłaniania (lag time), potrzebny do rozpadu podanej postaci leku oraz na uwolnienie i rozpuszczenie substancji leczniczej, to równanie 9.2 przyjmuje postać bardziej ogólną:

Można udowodnić, że równanie to jest równoważne wyrażeniu:

_c = Be^_K'—Ac^_k*'    (9.7)

Pozanaczyniowe podawanie leków 137