(14)

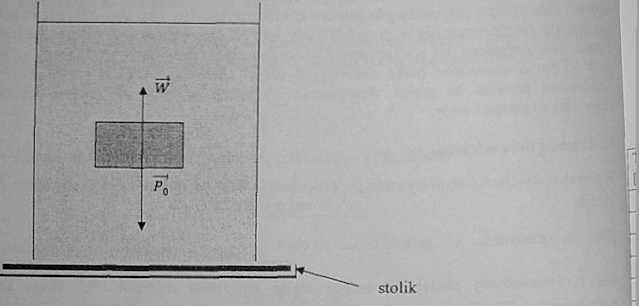
Nad szalką umieszczamy stolik . na którym ustawiamy naczynia wypełnione cieczą. W cw, zanurzamy badane ciało zawieszone na nilce przyczepionej do górnej części szalki. S musi mieć taką długość aby zanurzone w cieczy ciało nic dotykało dna naczynia. Jeżełjjjjj cieczy użyjemy wody destylowanej o gęstości A. to po zanurzeniu ciała w wofo równowaga będzie zachwiana. Na ciało oprócz siły ciężkości P₀ .działa teraz siła wyporu $ o wartości gdzie:

V-objętość zanurzonego ciała.

A. -gęstość wody w danej temperaturze (patrz tabela), g- przyspieszenie ziemskie.

Ponieważ siły P₀iW mają zwroty przeciwne, siła która działa na ciało po zanurzeniu w wodzie ma teraz wartość:

P_w=P₀-W = P_Q-V_Pttg.

Aby odzyskać równowagę musimy na szalce położyć odważniki o takiej masie ^m\. że ich ciężar ^mi£ zrównoważy siłę ,a zatem:

A ="».£.

Korzystając z przedstawionych wyżej zależności uzyskujemy układ równań:

vp_cg=pą~

Po podzieleniu równań stronami otrzymujemy:

t h _ Po % Po-py

skąd

Ar

Pe =

(na wadze) odważnikami o masie mo ■

Ponieważ siłę Pq równoważymy

- "*og ,

natomiast siłę P_w równoważymy odważnikami o masie fet

^p- ^=mi8,

po podstawieniu otrzymujemy:

Ipjl

w«og“«ig

W wyliczeniach nic musimy operować siłami (Po.P*) a jedynie masą odważników, które na wadze te siły równoważą. Pomiary przeprowadzamy dla dwóch ciał.

Wyniki pomiarów notujemy w tabeli:

Nr,	m0			pM ^:l	i llf
1
2
3
4
5					Si

Gęstość wody destylowanej, po wcześniejszym zmierzeniu jej temperatury (f_w), Odczytujemy z tabeli:

Zależność gęstości wody od temperatury 00*' —■).

ti	0	JL	2	3fl	4	Bi i			8 |	9 ;
i	0.9998*1	0.9999	0,99994	0.99996	0.99997	0,99996	0.99994	0.9999	059915	059978 |
10	0.9997	0.9996	0.9995	0.999)7;	0,99924	0,9991	0.99894	0.99877	0.9986	0.9984
20	0,9982	0,99799	099777	099753	0.99729	0.99704	0.99678	0.99651	059623	059594
30	0:9956'i	0.99534	Ó;9950iJ	0.9947	11 099437..	0.99403	0.99368	059333	0,99296	059259
40	0.9922J	0.99183,	0.99)44	0.99104	0.9906)	0.99022	058978	058937	0.98893	058849

Gęstość ciała jest średnią arytmetycznągęstości uzyskanych z pięciu kolejnych pomiarów:

I

3. Obliczenia niepewności pomiaru

Jeżeli pomiar powtórzymy co najmniej pięciokrotnie niepewność pomiaru możemy określić jako średnią niepewność kwadratową (Średnie odchylenie standardowe):

M n=5.

mm

B

/i(n

Wynik zapisujemy w postaci

Pe=Pc±&Pc

29