(4)

Niepewnością i-tego pomiaru będziemy nazywać

Ax_pi

X

p.

Teoria niepewności opracowana przez Gaussa pozwala na podstawienie wartości zmierzonych obliczyć pewną wartość * maksymalnie zbliżoną do wartości prawdziwej *>. Można udowodnić, że jest nią średnia arytmetyczna

n ' .

Różnicę

Ax_{ = Xt -r *

nazywamy niepewnością pozorną pomiaru, czyli odchyleniem wartości uzyskanej w i-tym pomiarze od średniego wyniku.

Gauss opracowując teorię błędów założył, że chodzi wyłącznie o niepewności przypadkowe oraz, że ich rozkład jest normalny tzn.:

•    niepewności małe występują w pomiarze częściej niż duże,

•    niepewności o znakach ujemnych są równie częste jak błędu o znakach dodatnich.

Teoretyczny rozkład wyników pomiarów przedstawia tzw. „krzywa dzwonowa"; zwana krzywą odchyleń Gaussa (1794 r.).

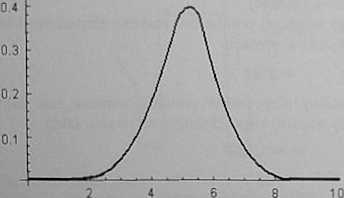
Dla dużej liczby pomiarów krzywa ta jest symetryczna.

Krzywa Gaussa jest krzywą w przyrodzie uniwersalną, taki rozkład można otrzymać analizując:

a)    wzrost np. mężczyzn,

b)    czas tycia muszek,

c)    prędkość cząsteczek gazu itd.

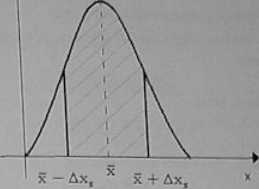
Przeprowadzając serię pomiarów o tym samym stopniu dokładności jako niepewność pomiaru można przyjąć tzw. średnie odchylenie standardowe średniej, zwane także średnią niepewnością kwadratową wartości średniej. Przez średnią niepewność kwadratową rozumiemy takie odchylenie pomiaru od wartości średniej że w zakreskowanym polu rozkładu Gaussa leży 68.3 % wszystkich pomiarów.

BI

u

Wartość średniej niepewności kwadratowej jest równa

^n(n-

Wynik pomiaru zapisujemy wtedy następująco

x = x ± Ax_a .

Chcąc skorzystać z tej metody obliczania niepewności pomiaru musimy wykonać serię co najmniej pięciu pomiarów.

b) Obliczanie niepewności maksymalnej pomiarów pośrednich

Rozważmy przypadek, kiedy pomiar jest stosunkowo mało dokładny i powtarzanie pom>itrów daje ten sam wynik lub pomiarów jest mało 2-3. W takim przypadku szacowanie niepewności dokonuje się na podstawie klasy przyrządu, a jeżeli klasa nie jest znana to zakładamy, że prawidłowy odczyt jest możliwy co najwyżej z dokładnością:

równa połowie najmniejszej działki, w jaką zaopatrzono skalę przyrządu.

Ogólnie jeżeli wynik pomiaru pośredniego y zależy od n wyników bezpośrednich powiązanych funkcją;

wtedy zmianę wartości dy związaną ze zmianami    obliczamy jako różniczkę zupełną:

dy = p.dx_{l +} ^.dx_{2 +} - + p-dx_n . dx_l ^x dx_z ²    dx_n *

a zastępując nieskończenie małe przez błędy A otrzymamy

| dtp \    \d<p I    t dtp I

M [t—|Ax_ł+ (•r-—|Ax₂+ •••+•—-

\dx₁

\dx

dxj

Ax,

Weźmy pod uwagę konkretne przykłady.

9