0061

62

I. Teoria granic

5) Wychodząc znowu od dwóch liczb dodatnich a i b {a>b), utwórzmy tym razem kolejno średnie arytmetyczne i średnie harmoniczne(¹):

a+b	hx	2 ab
2 ’		a + b
a i +6i	A	2flr b\_
2 ’		al+bl
On + bn 2 ’	bn+i	2 On bn On + bn

Na podstawie znanej nam już nierówności ~(a f b)> Vab (przy a+b) otrzymujemy

/a + b\²    a + b lab

I-I > ab, czyli --

a więc średnia arytmetyczna jest większa od średniej harmonicznej, a obie średnie zawierają się pomiędzy liczbami wyjściowymi. Stosując tę uwagę do a_n i b„, otrzymujemy

On^ a_n + i> b_n +1^> b„.

Zupełnie podobnie jak w przykładzie poprzednim przekonujemy się, że oba ciągi {a„} i !b„} dążą do wspólnej granicy c, którą można by nazwać średnią arytmetyczno-harmoniczną liczb a i b.

Tutaj jednakże granica c wyraża się prosto przez a i b. Mamy bowiem Cj =ab, a ponieważ podobnie a„ _{+ 1}b„₊₁=a„b„, więc wnioskujemy, że przy wszystkich wartościach n

a_nb„=ab.

Przechodząc do granicy, otrzymujemy

c

=y/ab,

tj. średnia arytmetyczno-harmoniczna dwóch liczb jest po prostu ich średnią geometryczną.

6) Przytoczymy teraz przykład bardziej złożony.

Wychodząc od pewnej liczby rzeczywistej c, przyjmijmy Xi=ic, a następne wyrazy ciągu {*„} określmy przez indukcję wzorem

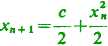
(1)

Zbadamy teraz zagadnienie zbieżności tego ciągu przy dwóch różnych założeniach o c.

Zauważmy, że gdybyśmy już wiedzieli, że istnieje skończona granica

(2)    a=limx„,

to można by ją znaleźć bez trudu. Wystarcza przejść do granicy w równości (1) określającej nasz ciąg, aby otrzymać

2

ca    ,

«=—+—, ^czyl‘ ^a —2a+c=0.

O Liczba c nazywa się średnią harmoniczną dwóch liczb dodatnich a i b, jeżeli jej odwrotność 1/c jest średnią arytmetyczną dla odwrotności 1 ja i 1 Ib: