Untitled 19

62

I. Teoria granic

[35

5) Wychodząc znowu od dwóch liczb dodatnich a i b (a>b), utwórzmy tym razem kolejno średnie arytmetyczne i średnie harmonicznej):

a + b	h.	lab
1 ’	^ ^U 1	a + b
ai -r b{	t>2	lav bt
2 ’		ai +bi
Qn~\~ bn	h ,	2an b„
i ’	Un + 1	&n “f* &n

Na podstawie znanej nam już nierówności j(a + b)>V ab (przy a^b) otrzymujemy

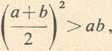
czyli

a + b lab

1 a + b a więc średnia arytmetyczna jest większa od średniej harmonicznej, a obie średnie zawierają się pomiędzy liczbami wyjściowymi. Stosując tę uwagę do a_n i b_n, otrzymujemy

an a_n +1b_n +1 b_n.

Zupełnie podobnie jak w przykładzie poprzednim przekonujemy się, że oba ciągi {«„} i {b_n} dążą do wspólnej granicy c, którą można by nazwać średnią arytmetyczno-harmoniczną liczb a i b.

Tutaj jednakże granica c wyraża się prosto przez a i b. Mamy bowiem a± b_t =ab, a ponieważ podobnie a_{n + 1}b_n+1=a„b„, więc wnioskujemy, że przy wszystkich wartościach n

a_n b_n = ab.

Przechodząc do granicy, otrzymujemy

’=Vab,

tj. średnia arytmetyczno-harmoniczna dwóch liczb jest po prostu ich średnią geometryczną.

6) Przytoczymy teraz przykład bardziej złożony.

Wychodząc od pewnej liczby rzeczywistej c, przyjmijmy x_x c, a następne wyrazy ciągu {*„} określmy przez indukcję wzorem

2

c x_n

U)

Zbadamy teraz zagadnienie zbieżności tego ciągu przy dwóch różnych założeniach o c.

Zauważmy, że gdybyśmy już wiedzieli, że istnieje skończona granica

(2)    a = lim*„,

to można by ją znaleźć bez trudu. Wystarcza przejść do granicy w równości (1) określającej nasz ciąg, aby otrzymać

2

ca    ₂

a=--j--, czyli a — 2a+c=0.

2 2

(^J) Liczba c nazywa się średnią harmoniczną dwóch liczb dodatnich a i b, jeżeli jej odwrotność 1/c jest średnią arytmetyczną dla odwrotności 1 la i 1/b:

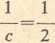
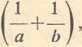
,    lab

skąd c=-

a + b