Untitled 15

58

I. Teoria granic

[33

skąd otrzymujemy (por. przykład 2))

(*+'>* ,

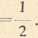
lim — lim

2 ⁿ +-(k-\-i)kn^k 1 + ...

§ 3. Ciąg monotoniczny

34. Granica ciągu monotonicznego. Przytaczane dotąd twierdzenia o istnieniu granicy ciągu miały następujący- charakter: przy założeniu, że pewne ciągi posiadają granice, wnioskowano o istnieniu granic dla innych ciągów, ale w pewien sposób powiązanych z poprzednimi. Nie stawiano natomiast pytania o kryteria istnienia skończonej granicy dla danego ciągu, danego bez związku z innymi ciągami. Pozostawiając rozwiązanie tego pytania w ogólnej postaci do § 4, ustępy 39 - 42, rozważmy teraz ogólną i ważną klasę ciągów, dla których można to zagadnienie łatwo rozwiązać Ciąg {x„} nazywamy ciągiem rosnącym, jeżeli

x₁<x₂<...<x„<x„₊₁<... ,

tj. jeżeli przy ri>n mamy x„< >x_n. Ciąg nazywamy ciągiem niemalejącym, jeżeli

tj. jeżeli z n >n wynika tylko x„.^x_n. Ciągi te nazywamy także rosnącymi w szerszym sensie.

Podobnie ustalamy pojęcie ciągu malejącego — w węższym lub szerszym sensie. Nazywamy tak ciąg, dla którego jest odpowiednio

x₁>x₂>...>x„>x_n+1>...

lub

x₁^x₂^...^x_n>x_{n + 1}^...,

a więc z n’>n wynika (zależnie od definicji) x„.<x_rt lub tylko x_n>^x„.

Ciągi wszystkich tych rodzajów nazywamy ogólnie ciągami monofonicznymi. Zwykle mówimy o ciągu, że monofonicznie rośnie lub monofonicznie maleje.

Dla ciągów monotonicznych jest słuszne następujące ważne twierdzenie: Twierdzenie. Niech dany będzie monofonicznie rosnący ciąg {x„}. Jeżeli ciąg fen jest ograniczony z góry:

x„<M (M=const; n = 1,2,3, ...),

to ma granicę skończoną, a w przeciwnym przypadku dąży do +oo.

Podobnie zawsze ma granicę monofonicznie malejący ciąg {x„}. Granica ta jest skończona, jeżeli ciąg jest ograniczony z dołu:

x„^m (m = const; n — 1,2,3, ...),

a w przeciwnym przypadku granicą jest — oo.