0203

204

III. Pochodne i różniczki

co umożliwi nam wykorzystanie przykładu 2) (i reguł ogólnych, o których wspominaliśmy na początku). Ostatecznie

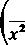
¹    f ^1    1    1

Ta²) Ta Y(x-af^ri~ (x + a)^{n + i}\

7) W przypadku funkcji y=e“^x&inbx zastosujemy bardziej sztuczny sposób. Mamy mianowicie

y' = ae°* sin bx + be^ax cos bx ; jeśli wprowadzimy kąt pomocniczy ę wyznaczony przez warunki

b    a

sin <p= —------------ , cos q> =    -------,

s] a²+ b²    yf a² -\-b²

to pierwszą pochodną będziemy mogli napisać w postaci

y'a² + b² e“(sin bxcos p+cos ójcsin <p)=yja²+b² e“*sin (bx+ ę).

Powtarzając różniczkowanie możemy łatwo wyprowadzić ogólne prawo

yⁱⁿ⁾ — (a² +b²y^,2e°^x sin (bx + nq>)

i udowodnić je metodą indukcji matematycznej.

8) Zatrzymamy się jeszcze na funkcji y—arc tg x. Postawimy sobie na wstępie za zadanie wyrazić y^m przez y. Ponieważ x — tgy, zatem

y'=-,=cos² y=cosy sin(y-firc) .

1+Jt

Różniczkując powtórnie względem x (i pamiętając, że y jest funkcją x) otrzymamy

y"= [—sinysin(y+}n)+cosł>cos(y+ł jt)]y'=cos²>'cos(2>'+i jt)=cos²ysin2(y+in).

Następne różniczkowanie da nam

y‘"= [—2sinycosySin2(y+in)+2cos²ycos2(>’+iir)]y^,= =2cos³ycos(3y+2-in)=2cos³ y sinSfy+Jii).

Ogólny wzór

y^M=(.n — 1) !cos"ysin«(y+i7t)

można udowodnić metodą indukcji matematycznej.

Jeśli (dla x> 0) wprowadzimy kąt

1 1

z=arc tg —=— n—y , x 2

to wzór ten można napisać tak:

^"*=(71 — 1) 1-sin n(n—z)

(l+ar²)"'²

lub ostatecznie

(1 +x²f²

=(—l)”^-1 (n — 1) !

sin arc tg —j .

9) Jako ćwiczenie wyprowadzimy na zakończenie wzór

(«=1,2,...).

e^t,x

£_V-_V/,₎₌(_1).__