0245

246

IV. Badanie funkcji za pomocą pochodnych

3) Znaleźć ekstrema funkcji f (x)=x^2l3—(x¹ — l)¹¹³. Tym razem pochodna skończona

/'(*)=!aT^,/3—i(x² —1)

•2/3

2x=

(.x²-lf³-x^4/3

x‘'V-l)^2/3

istnieje wszędzie oprócz punktów x=0 i *= ± 1.

Przy zbliżaniu się x do tych wartości (z obu stron) pochodna dąży do ±<x>.

Dla wyznaczenia pierwiastków pochodnej przyrównajmy do zera jej licznik; otrzymamy x=± 1/^/2. Tak więc „podejrzane” o ekstremum są punkty

1 1

-1, 0, —, V 2    V²

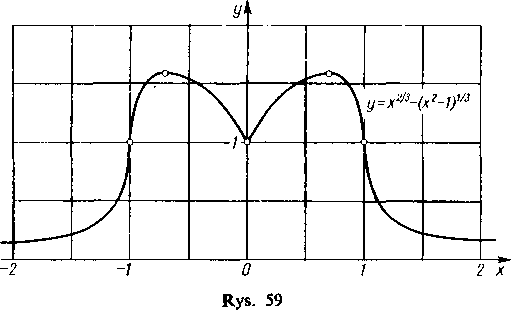
W punkcie x=0 i w pobliżu tego punktu licznik i drugi czynnik mianownika mają znak plus, natomiast czynnik x^l/3 w mianowniku zmienia znak z minusa na plus. Tak samo zachowuje się pochodna, mamy więc minimum. W punkcie x= 1/^/2 (i w pobliżu) mianownik zachowuje znak plus. Ponieważ chodzi nam o wartości x bliskie 1/^/2, przepiszmy licznik w postaci (1 — x²)²'³ — x*¹³; jest on równy zeru dla x=\!_sJl. Gdy zmniejszymy x, licznik się powiększa, a gdy powiększymy x, licznik się zmniejsza, a więc zmienia on znak z plusa na minus, mamy tu zatem maksimum. Tak samo jest również w punkcie x= —llyj2. Przy przejściu przez x=l czynnik (x² —1)^2/3 w mianowniku, który w punkcie tym znika, nie zmienia znaku; to samo dotyczy również pochodnej, tak że w punkcie x=l nie ma ekstremum. To samo w punkcie x=— 1.

Tak więc maksima wynoszą/(±l/^/2)=³1(/4«l,59, a minimum /(0)=1.

Wykres zamieszczamy na rys. 59 (porównaj ustęp 149, 4)).

4) Drgania tłumione. Niech ruch punktu odbywa się według prawa

s=Ae~^ktsin cot,

gdzie s jest drogą przebytą liczoną od położenia początkowego, a t — czasem liczonym od chwili początkowej. Będziemy uważali, że wszystkie stałe A, k, ta, jak również zmienna t są dodatnie. Wyjaśnimy, jaką postać ma wykres tej zależności; będzie rzeczą ciekawą porównać go ze znaną nam już sinusoidą s=A sin cot. Ponieważ e"“>0, oba wykresy przecinają oczywiście oś x w tych samych punktach t—nnlco (»= 1, 2, 3, ...). Zauważmy, że funkcja s=A sin cot ma na przemian mhksima i minima w‘punktach t=(n+i) njco, w których znika jej pochodna s'=Aco cos cot. Obliczmy pochodną danej funkcji (porównaj ustęp 99, 30))

s' —Ae~^k\cocos cot—k sincot)=A J co¹ +k² e~^kt (    cos cot--,    - sin cot

Kyf^Tk² V^+F