0251

252

IV. Badanie funkcji za pomocą pochodnych

139. Znajdowanie wartości największych i najmniejszych. Niech funkcja /(x) będzie określona i ciągła w skończonym przedziale domkniętym <0, b}. Do chwili obecnej interesowaliśmy się tylko jej maksimami i minimami, teraz zajmiemy się zagadnieniem znajdywania wartości największej i wartości najmniejszej ze wszystkich, które funkcja ta przybiera w tym przedziale (^x); zgodnie z drugim twierdzeniem Weierstrassa [85] takie najmniejsze i największe wartości istnieją. Zatrzymamy się na przypadku wartości największej.

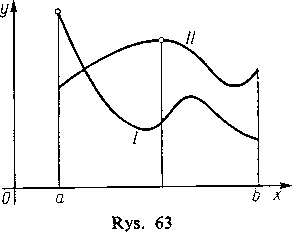
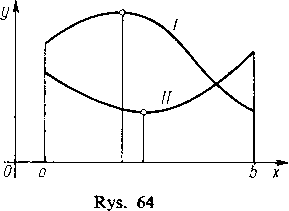
Jeśli funkcja osiąga wartość największą w pewnym punkcie pośrednim między punktami a i b, to będzie to jednocześnie jedno z maksimów (oczywiście największe); ale największa wartość może być osiągnięta również na jednym z końców przedziału, tzn. w a lub b (rys. 63). Tak więc trzeba porównać ze sobą wszystkie maksima funkcji /(x) i jej wartości na końcach przedziału f{a) oraz f(b); największa z tych liczb będzie właśnie największą wartością funkcji f(x) w przedziale <a, ń>. W podobny sposób znajdujemy również najmniejsze wartości funkcji.

Przypuśćmy na przykład, że szukamy wartości największej i najmniejszej funkcji f(x)=sin³ jc+cos³¹ w przedziale <—dwa maksima równe 1 są większe od wartości, które przyjmuje funkcja na końcach przedziału: /(—^«)=/(jit) = 0. Wobec tego 1 jest największą wartością funkcji w danym przedziale. Minimum równa się 0,7 ..., jest więc ono większe od wartości funkcji na końcach przedziału, a zatem najmniejszą wartością jest 0. Dla przedziału <jłi, |łt> należy przyjąćja ko największą wartość większe z dwóch maksimów 1 i —0,7 które funkcja ta osiąga w punktach x=|n i ~it, na końcach przybiera ona bowiem wartości /(jłt) = 0,7 ... i/(|n)=—1, tzn. mniejsze niż 1. Najmniejszą wartość osiąga funkcja na prawym końcu oraz dla x=n, gdzie ma ona minimum.

Jeśli pragniemy uniknąć badania funkcji na maksimum lub minimum, to można postąpić inaczej. Trzeba tylko obliczyć wartości funkcji we wszystkich punktach podejrzanych o ekstremum i porównać te wartości z wartościami /(o) i f(b), które funkcja przybiera na końcach przedziału; największa i najmniejsza z tych liczb będzie oczywiście odpowiednio największą i najmniejszą wartością funkcji.

Na przykład dla przedziału <—porównujemy wartości /(O) =1, /(Jjt)=0,7 ...,/(|tt) = l z wartościami na końcach przedziału /(—^»t)=/(|jt) = 0, a dla przedziału    porównujemy

liczby /(ijr) = l, /(n)=— 1, /(^jt)= —0,7 ..., z wartościami na końcach przedziału /(ijt)=0,7 ...

i/(f¹)=-T

1

W ten sposób termin maksimum zachowuje swój „lokalny” sens (największa wartość w bezpośrednim otoczeniu odpowiedniego punktu); odróżniamy maksimum od największej wartości funkcji w całym rozpatrywanym przedziale.

To samo dotyczy również minimum i najmniejszej wartości funkcji.