0265

266

IV. Badanie funkcji za pomocą pochodnych

Pierwsza z tych nierówności pokrywa sięjednakz nierównością (10), z ustępu 143(należy uwzględnić podaną tam uwagę). Druga z tych nierówności jest odpowiednikiem nierówności (10) dla funkcji wklęsłej.

Uwaga. Tę własność krzywej przyjmuje się często za definicję punktu przegięcia. Taka definicja nie jest wcale równoważna z tą, która była dana wyżej. Przede wszystkim krzywa może nie mieć stycznej w punkcie przegięcia, a więc druga definicja może okazać się niestosowalna. Może się zdarzyć i na odwrót: krzywa przecina styczną w punkcie, który nie oddziela wypukłej części krzywej od części wklęsłej, wówczas pierwsza definicja nie może być zastosowana. Takie są krzywe na rysunkach 43c i d. Jeszcze ciekawsza jest jednak krzywa

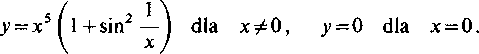
Jest ona styczna w początku współrzędnych do osi x i przecina ją. Istnieje tu nawet druga pochodna ciągła, ale zmienia ona znak nieskończenie wiele razy w pobliżu punktu x=0, zarówno z lewej, jak i z prawej strony.

§ 3. Konstrukcja wykresów funkcji

146. Postawienie zagadnienia. Uzbrojeni we wszystkie metody rachunku różniczkowego powrócimy obecnie do zagadnienia konstrukcji wykresów funkcji (porównaj ustęp 47). Przypuśćmy najpierw, że trzeba zbudować wykres funkcji y=f(x) ciągłej w przedziale skończonym <a,ń>. Przy tym zasadniczym naszym celem jest teraz możliwie dokładne scharakteryzowanie samego przebiegu zmiany funkcji, dokładność zaś poszczególnych rzędnych interesuje nas w mniejszym stopniu.

Stosowany zwykle sposób konstrukcji według punktów [47], które wybieramy gęściej lub rzadziej, lecz przypadkowo i bez związku z (nieznanymi z góry) własnościami wykresu jest nieprzydatny. Wymaga on przede wszystkim obliczenia dużej ilości rzędnych, co praktycznie jest niewygodne. Główna przyczyna jest jednak inna — sposób ten jest nieprzydatny ze względów zasadniczych, gdyż właśnie z powodu przypadkowości wyboru obliczanych rzędnych nie zapewnia on osiągnięcia zamierzonego celu.

Załóżmy teraz, że funkcja y=f{x) ma na ogół pochodną skończoną y'=f'(x). Wyjątek mogą stanowić tylko poszczególne punkty, w których pochodna może być nieskończona. Wówczas metody rachunku różniczkowego dają możność znalezienia pewnej liczby punktów podstawowych, charakterystycznych dla tego właśnie wykresu, za pomocą których wykres można skonstruować już z wystarczającą dokładnością.

Mamy tu na myśli przede wszystkim punkty zwrotne wykresu, tzn. wierzchołki jego wzniesień i zagłębień, odpowiadające wartościom ekstremalnym funkcji [134- 138], Poza tym trzeba do nich dołączyć wszystkie w ogóle punkty, w których styczna jest pozioma lub pionowa, nawet jeśli nie odpowiadają im ekstrema funkcji. Powinny być zaznaczone, rzecz jasna, również końce wykresu.