0269

270

IV. Badanie funkcji za pomocą pochodnych

stron od x₀ (jeśli x₀ nie jest końcem przedziału) funkcja może mieć granice różnych znaków. W każdym wypadku wykres uciekając w nieskończoność będzie się nieograniczenie zbliżał do pionowej prostej x=x₀ w jej górnej lub dolnej części, zależnie od znaku granicy nieskończonej. Prosta ta pozwala dokładnie wyobrazić sobie wygląd wykresu poza obrębem

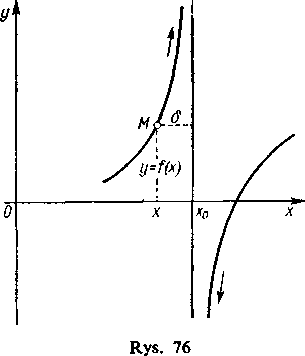
rysunku (rys. 76). Jako przykłady mogą służyć znane nam już wykresy funkcji y=ajx dla x=0 (rys. 10), y=tgx dla x=(2k+ l)^7t (rys. 16) oraz y = log,,* dla x=0 (rys. 14).

W przypadku przedziału nieskończonego (w jedną albo w obie strony) w podobnym celu można się posłużyć czasami prostą poziomą lub pochyłą, do której wykres przybliża się nieograniczenie. W związku z tym podamy następującą ogólną definicję.

Niech będzie dana krzywa, której gałąź oddala się w tym czy w innym kierunku do nieskończoności. Jeśli odległość <5 od punktu krzywej do pewnej określonej prostej dąży do zera w miarę oddalania się punktu do nieskończoności, to prosta ta nazywa się asymptotą krzywej.

Przed chwilą mieliśmy do czynienia z asymptotami pionowymi; zajmiemy się teraz asymptotami poziomymi i pochyłymi - zawsze dla krzywej określonej równaniem y =/(*).

Przykłady asymptot poziomych spotkaliśmy już: dla krzywej y=a/x taką asymptotą jest prosta y=0 przy x-+ + oo (rys. 10), dla krzywej y=arc tg x - proste y=%k i y = - in, zależnie od tego, czy x-» + oo czy x-> — co (rys. 21), dla krzywej y=a^x — prosta y=0 przy x-+ — oo, jeśli a> 1 i przy x-> + oo, jeśli a< 1 (rys. 13).

Na to, żeby na przykład przy x-> + co prosta Y—b była asymptotą krzywej y =f (x) oczywiście potrzeba i wystarcza (rys. 77), żeby

lim <5= lim |y — b| = 0 lub lim y= lim f(x) = b.

*-►+00 *-*• + 00 X-> + 00 *-> + 00

W ten sposób zagadnienie znalezienia asymptoty poziomej sprowadza się po prostu do znalezienia tej granicy.

Oddzielnie trzeba szukać podobnej granicy także dla x-»-co; możemy przy tym (jak na przykład w przypadku krzywej y=arc tg x) otrzymać inną asymptotę.

Przechodząc do asymptot pochyłych przypominamy, że jako przykłady mogą służyć

znane czytelnikowi z geometrii analitycznej asymptoty y=± — x hiperboli

✓ X² y² b r^i-T

(1) -j—j = l lub y=±—\x² — a²

ab a

(patrz także rys. 7 na str. 85).