0277

278

IV. Badanie funkcji za pomocą pochodnych

Zwracamy uwagę czytelnika na to, że tu także i stosunek pochodnych był znowu wyrażeniem nieoznaczonym typu 0/0, ale okazało się, że tę nieoznaczoność udało się obliczyć za pomocą przekształceń elementarnych. W innych wypadkach może się okazać, że twierdzenie trzeba zastosować powtórnie. Podkreślamy, że dozwolone są przy tym wszelkie uproszczenia otrzymanych wyrażeń; skracanie przez wspólne czynniki, wykorzystanie znanych nam już granic itp. (Tego wszystkiego nie wolno było robić, gdy stosowaliśmy twierdzenie 2!). W następnym przykładzie twierdzenie 3 stosuje się trzykrotnie; po pierwszym różniczkowaniu skracamy przez e^x, a po drugim odrzucamy czynnik e* w mianowniku (ponieważ dąży on do 1). Upraszcza to obliczenia.

lim

X-*0

2xe^2x+e^2x++e^x-4e^2x+2e^x 3(e'-l)²e*

xe² +xe —2e² +2e Przykład 5. lim---₅-

i-o    (e -1)

= lim

x-»0

2xć^x — 3e*+3+jt 3(e*-.l)^J

1

— lim 3 i-o

2xe^x+2e^x—2e^x+l

2(e^x-l)e^x

lim

I-O

-e^x+2xe^x+\

(e^x-i)e^x

1

=— lim 6 i-o

2xe^x + e

1

6"

lim

1-0

x—(1 +x)ln(l +x) x²(l +x)

Przykład 6.

(1 +x)^llx—e

X

lim (1 +x)^tlx

x-*0

Ponieważ pierwszy czynnik z prawej strony dąży do e, więc wystarczy zająć się drugim czynnikiem. Stosując dwukrotnie twierdzenie 3 znajdziemy, że jego granica równa się —

Odpowiedź: —Je.

Twierdzenie 3 można łatwo rozszerzyć na przypadek, gdy argument x dąży do granicy nieskończonej: a= ±oo (tego, rzecz jesna, nie można zrobić w stosunku do twierdzeń 1 i 2).

Twierdzenie 3*. Niech: 1) ftmkcje f{x) i g(x) będą określone w przedziale (c, +oo), gdzie c>0, 2) lim f{x) = 0, lim g(x)=0, 3) istnieją w przedziale <c, + oo) pochodne skon-

X-* 00    X-* 00

czone f'(x) i g’(x), przy czym g'(x)=£0, wreszcie 4) istnieje granica {skończona lub nieskończona)

lim

x~* + oo

/'(*)

9\x)

Wtedy

lim

+ 00

/(*)

9(x)

Dowód. Przekształcimy zmienną x według wzoru x—l/t, t=l/x. Wtedy, jeśli x~* +oo, to 0, i na odwrót. Ze względu na 2) mamy

lim f(—)=0, lim g )=0,

(-+0 \t /    |->+0 \ t J

a na mocy 4):

lim

(- + 0

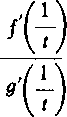
= K.