0289

290

IV. Badanie funkcji za pomocą pochodnych

Mamy

f(x)=xⁱ-2x²-Ax-l ,    /(3)=-10<0,    /(4)=+9>0,

f'(x) — 2x² — 4x — 4>0 , f"(x) = 6x—4>0 (dla 3<x<4)

(przypadek I); najmniejszą wartością |/'(x)| jest m= 11.

Bierzemy za punkt wyjścia koniec b — 4 danego przedziału, w którym znak funkcji /(x) jest zgodny ze znakiem /"(*). Na mocy wzoru (8)

m

/'(4)

=4_-=4-0,32... 28

zaokrąglając weźmy xj = 4 —0,3 = 3,7. Ponieważ/(x\)=f (3,7)= 1,473, otrzymamy na mocy nierówności 1,473

(6) xj—£<——<0,14, tzn. osiągnięta dokładność nie wystarcza. Mamy dale

3,7-0,066... ;

. ,, fOJ)    1,473

*2=3,7---=3,7---

/'(3,7)    22,27

przyjmijmy x\ = 3,7—0,066 = 3,634. Tym razem/(x'₂)=/(3,634) = 0,042..., a więc na mocy (6) x'₂—i< 0,042

<———<0,004. Dlatego 3,630<ć<3,634 i £ = 3,63 z żądaną dokładnością.

Otrzymanie tego samego wyniku w ustępie 154 metodą siecznej wymagało trzech kroków.

2) Jako drugi przykład rozwiążmy równanie

xlogi₀x=l

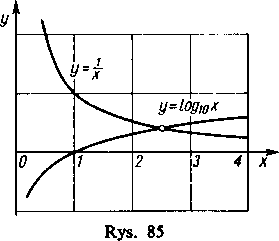
Skorzystamy z okazji, żeby objaśnić czytelnikowi, jak wykres funkcji może pomóc nam w uprzednim zorientowaniu się, gdzie leżą pierwiastki równania. Wartość x spełniająca równanie

1

logio ■*=—

x

jest oczywiście odciętą punktu przecięcia krzywych

1

y = logi₀ X    i y=— .

x

Nawet wykonany z grubsza wykres (rys. 85) pokazuje od razu, że szukany pierwiastek leży między liczbami 2 i 3. Łatwo jest to sprawdzić teraz także rachunkiem, biorąc bowiem f(x)=x logio x-1, mamy

/(2)=-0,39793...<0 ,

/(3)=0,43136... >0 .

Obliczymy wspomniany pierwiastek z dokładnością do 0,0001.

Dla 2<x<3 mamy oczywiście

/'(x)=log,₀x + log₁₀e>0 ,

logio e

(przypadek I); można przyjąć m = 0J.

x

/"(*) >0