0291

292

IV. Badanie funkcji za pomocą pochodnych

a więc zbliżamy się do żądanej dokładności. Następne przybliżenie

0,031144...

=0,30----

0,8533643... —4

= 0,30

0.031144... 3,1466356...

=0,309897...

zaokrąglamy do piątego znaku „w stronę pierwiastka” x₂ = 0,30990. Ponieważ mamy /(0,30990) = = 0,000021 ...>0, wartość ta jest wciąż mniejsza od pierwiastka. Błąd tego przybliżenia wynosi na mocy (6):

0,000022

x₂<--<0,00001 ,

3

a więc ostatecznie 4) Równanie

£ = 0,30990 + 0,00001 . tgA- = x

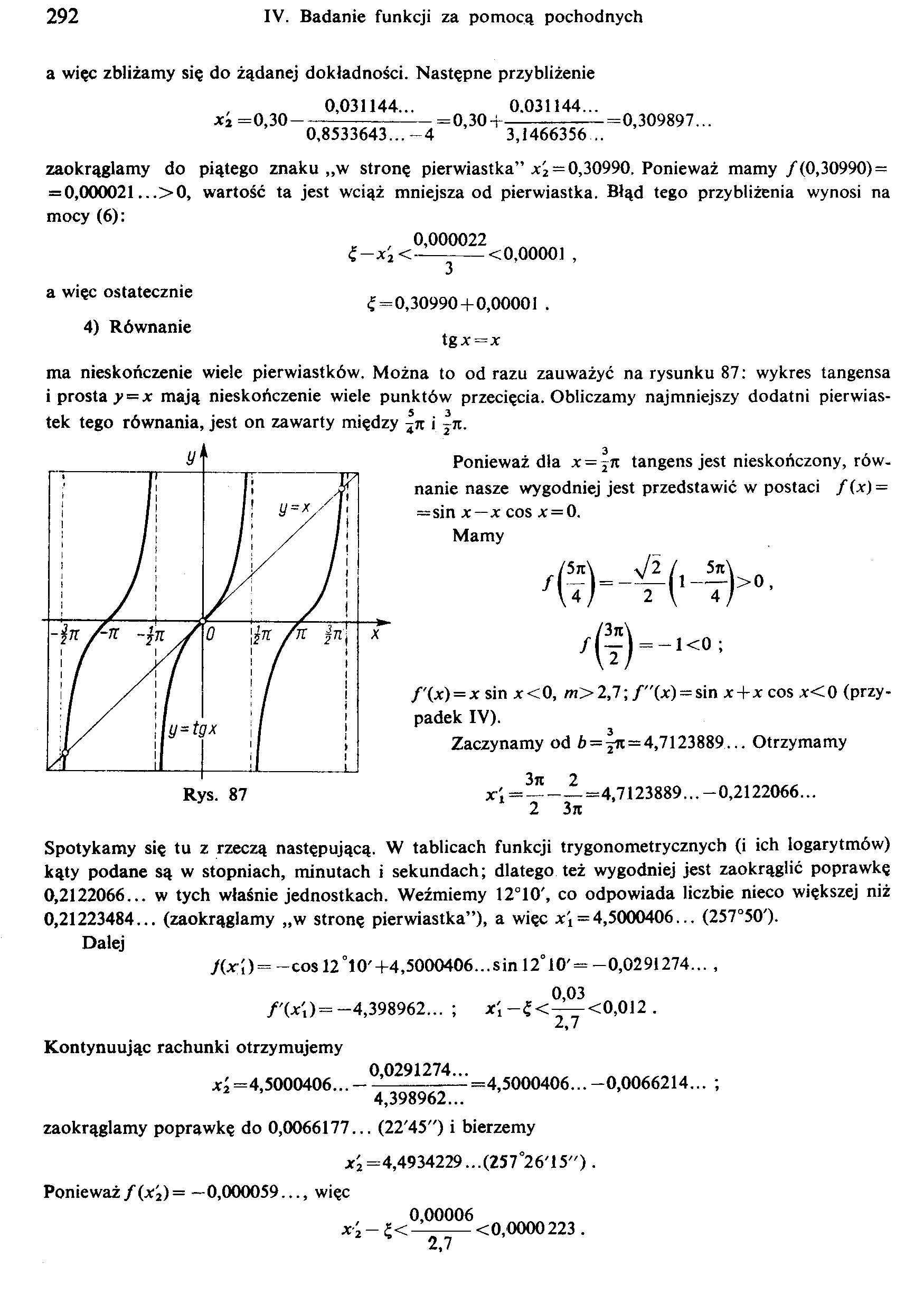
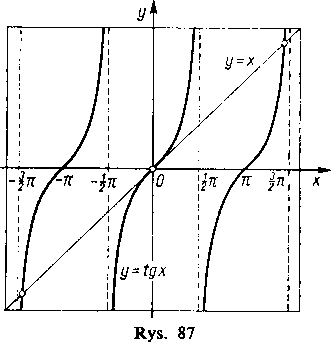
ma nieskończenie wiele pierwiastków. Można to od razu zauważyć na rysunku 87: wykres tangensa i prosta y=x mają nieskończenie wiele punktów przecięcia. Obliczamy najmniejszy dodatni pierwiastek tego równania, jest on zawarty między |jr i ~it.

3

Ponieważ dla x= ₂n tangens jest nieskończony, równanie nasze wygodniej jest przedstawić w postaci / (x) = =sin x—x cos .* = 0.

Mamy

f'(x) = x sin x<0, m>2,7; /"(*) = sin x+x cos x<0 (przypadek IV).

Zaczynamy od 6 = ^ = 4,7123889... Otrzymamy

x', = — - — =4,7123889... -0,2122066...

2    3 n

Spotykamy się tu z rzeczą następującą. W tablicach funkcji trygonometrycznych (i ich logarytmów) kąty podane są w stopniach, minutach i sekundach; dlatego też wygodniej jest zaokrąglić poprawkę 0,2122066... w tych właśnie jednostkach. Weźmiemy 12°10', co odpowiada liczbie nieco większej niż 0,21223484... (zaokrąglamy „w stronę pierwiastka”), a więc x\ = 4,5000406... (257°50')-Dalej

J(x\)= -cos 12°10' +4,5000406...sin 12°10'= -0,0291274... ,

0,03

/'(*',)= -4,398962... ;    x\-£<— <0,012 .

Kontynuując rachunki otrzymujemy

0 0291274

x₂ =4,5000406... - -- =4,5000406... -0,0066214... ;

4,398962...

zaokrąglamy poprawkę do 0,0066177... (22'45") i bierzemy

x'i =4,4934229...(257°26'15").

Ponieważ f(x'₂) = —0,000059..., więc

0,00006

x'₂-Ł<--<0,0000223 .

²    ^    2,7