0308

309

§ 1. Pojęcia podstawowe

Wprowadzimy jeszcze kilka terminów. Zbiór punktów Jt nazywa się ograniczony, jeśli zawiera się całkowicie w pewnym prostopadłościanie.

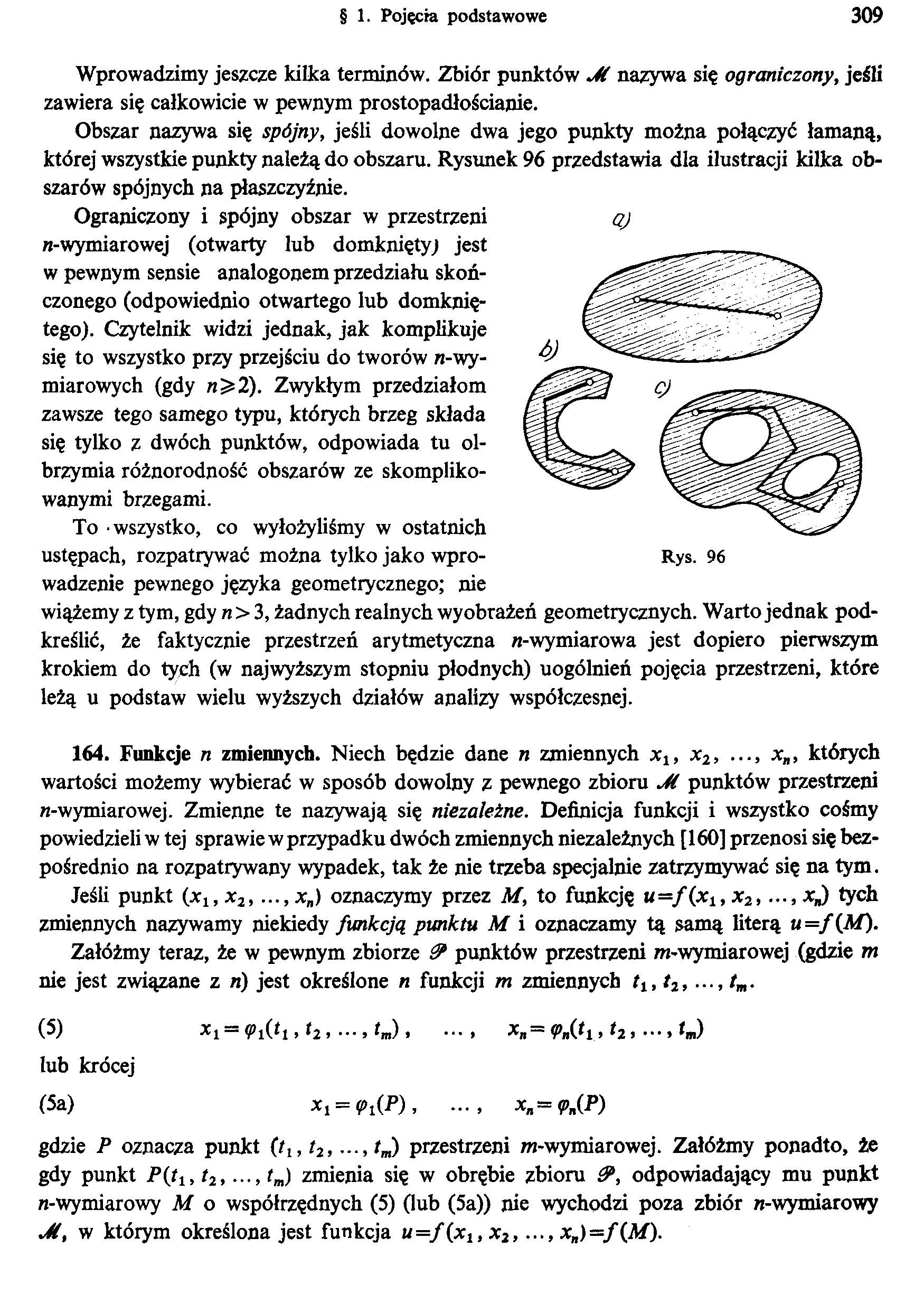
Obszar nazywa się spójny, jeśli dowolne dwa jego punkty można połączyć łamaną, której wszystkie punkty należą do obszaru. Rysunek 96 przedstawia dla ilustracji kilka obszarów spójnych na płaszczyźnie.

Q)

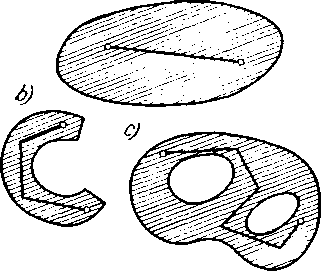
Rys. 96

Ograniczony i spójny obszar w przestrzeni n-wymiarowej (otwarty lub domknięty) jest w pewnym sensie analogonem przedziału skończonego (odpowiednio otwartego lub domkniętego). Czytelnik widzi jednak, jak komplikuje się to wszystko przy przejściu do tworów n-wymiarowych (gdy «5=2). Zwykłym przedziałom zawsze tego samego typu, których brzeg składa się tylko z dwóch punktów, odpowiada tu olbrzymia różnorodność obszarów ze skomplikowanymi brzegami.

To wszystko, co wyłożyliśmy w ostatnich ustępach, rozpatrywać można tylko jako wprowadzenie pewnego języka geometrycznego; nie wiążemy z tym, gdy n > 3, żadnych realnych wyobrażeń geometrycznych. Warto jednak podkreślić, że faktycznie przestrzeń arytmetyczna «-wymiarowa jest dopiero pierwszym krokiem do tych (w najwyższym stopniu płodnych) uogólnień pojęcia przestrzeni, które leżą u podstaw wielu wyższych działów analizy współczesnej.

164. Funkcje n zmiennych. Niech będzie dane n zmiennych x₂, x₂, ..., x„, których wartości możemy wybierać w sposób dowolny z pewnego zbioru M punktów przestrzeni n-wymiarowej. Zmienne te nazywają się niezależne. Definicja funkcji i wszystko cośmy powiedzieli w tej sprawie w przypadku dwóch zmiennych niezależnych [160] przenosi się bezpośrednio na rozpatrywany wypadek, tak że nie trzeba specjalnie zatrzymywać się na tym.

Jeśli punkt (jc_ł, x₂,..., x„) oznaczymy przez M, to funkcję u=f(x_ltx₂, ■■■, x_n) tych zmiennych nazywamy niekiedy funkcją punktu M i oznaczamy tą samą literą u =f(M).

Załóżmy teraz, że w pewnym zbiorze & punktów przestrzeni m-wymiarowej (gdzie m nie jest związane z n) jest określone n funkcji m zmiennych t_lt t₂,, t_m.

(5)    Xi = <Pi(ti , t₂,, t_m),    ..., x_n= (p_n(t₂, t₂,..., t_m)

lub krócej

(5a)    x_i = <p_t(P),    ..., x_n=ę>_n(P)

gdzie P oznacza punkt (/,, t₂,..., t_m) przestrzeni m-wymiarowej. Załóżmy ponadto, że gdy punkt P(t₂, t₂,..., t_m) zmienia się w obrębie zbioru 9, odpowiadający mu punkt n-wy miarowy M o współrzędnych (5) (lub (5a)) nie wychodzi poza zbiór n-wymiarowy M, w którym określona jest funkcja u=f(x₁, x₂, ..., x„)=f(M).