036 (8)

Zadania dodatkowe

.    ,v + 2

Ponadto mianownik ułamka ^    ^ musi być różny od zera. czyli .y - 4 * 0.

Uzyskujemy układ nierówności:

.v -4 .v - 4 * 0

«- zastępujemy iloraz iloczynem, bo interesuje nas znak wyrażenia

( (.y + 2)(.y - 4) > 0

.y * 4

x = -2 lub ,y = 4 .Y * 4

Znalezione liczby zaznaczamy na osi liczbowej i rysujemy pomocniczy wykres.

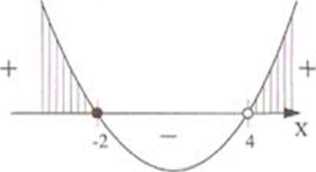
Ponieważ znak nierówności jest >. szukamy części wykresu znajdującego się nad osią OX i odpowiadających im przedziałów. Szukanymi przedziałami są (-x, -2] u (4, +x).

Czyli

x e (-x, -2] u (4, +x)

Wyznaczona suma przedziałów jest dziedziną drugiej funkcji.

Aby znaleźć dziedzinę funkcji podanej w temacie zadania, trzeba teraz wyznaczyć część wspólną dziedzin funkcji składowych.

Dziedzina pierwszej funkcji: .v € ( x, 5) kj (0, 6)

Dziedzina drugiej funkcji: x e (-cc, -2] u (4. +x)

Część wspólna:

-1				L	■Y > 0_			.Y>	- 1
H			n					1	□	1 ^
	5		1 !	M 2	1 ? 1 0	i		4		V 6 ^X

y € (-x, -5)    (4_t 6)

Odpowiedź

Dziedziną podanej funkcji jest zbiór (-x, 5) u (4, 6).

ZADANIE 14

Dany jest ciąg o wyrazie ogólnym a_n

Dla jakiej wartości parametru p granicą tego ciągu jest większa z liczb spełniających równanie

log2 + log(4* ¹ + 9) = 1 + log(2*^: + 1)

Rozwiązanie:

Najpierw rozwiążemy równanie

log2 + log(4^v_: + 9) = 1 + log(2^v: + 1)

Wyznaczamy dziedzinę równania:

wynika z definicji logarytmu. liczba logarytmo-wana musi być dodatnia

jest tak dlatego, że funkcja wykładnicza przyjmuje tylko wartoici dodatnie

f 4*¹ + 9 > 0 } 2*¹ + I > 0

{.v € R I x e R

Dziedziną równania jest zbiór liczb rzeczywistych, .v e R.

Teraz rozwiązanie równania

log 2 + log (4*¹ + 9) - I + log (2*“¹ + 1)

(wszystkie logarytmy są dzx*siętne_f stąd J = log 10)

log 2 + log (4*¹ + 9) = log 10 + log (2*"^: + I)

log [2 • (4'¹ + 9)] = log (10(2'¹ + 1)]

2(4*¹ + 9) = 10(2' ¹ + l)

2 -4' ¹+ 18= 10- 2* ¹+ 10 2 • 4‘¹ + 18-10-2*¹ -10 = 0 2-4' :4¹ + 18- 10-2* :2¹- 10 = 0

korzystamy ze wzoru

log p + log/ = log/6 • ó.

skoro logarytmy są równe, to liczby logarytmo-wane też

korzystamy ze wzoru a* " ^c a’: a^f

71

1

   18-io 10 = 0

2 • 77 + 18-10-^7-10 = 0 /• 16 16    4