0419

420

VI. Wyznaczniki funkcyjne i ich zastosowania

W tym celu znajdziemy najpierw metodą.Lagrange’a wszystkie ekstrema warunkowe. Funkcja pomocnicza

(ax² +by² +cz²)²

+ 2(x + y +z )

prowadzi do równań

x [(a²-{-A)^2a(ax² +by² J_rcz²)]=0 , y [(ó² + ż) — 2b(ax² + by² +cz²)]=0 , z l(c²s-2) — 2c(ax² + by² +cz²)]=0 ,

do których należy jeszcze dołączyć równanie stanowiące warunek dodatkowy. Stąd

(ł)	x=0,	F=0,	r=±l	(«=0j;
(II)	x=0,	F=±l ,	z—0	(«=0);
(III)	*=±1	, y=0,	Z = 0	(«=0) ;
(IV)	x=0, y=	1 ±-p. n/2		(«=i(ó-c)^2) ;
(V)	1 V2	1 P = 0, ^z=±-7= V2		(u=i(a-c)^2);
(VI)	1 *=±-7=.	1 y=±-p, z=0		(«=i(fl-ó)^2)

n/2

Wybierając z podanych w nawiasach wartości u najmniejszą i największą, otrzymamy rozwiązanie zadania [por. 200, 2)].

3) Wróćmy do zadania o najekonomiczniejszych przekrojach przewodów w sieci elektrycznej z połączeniem równoległym [201, 8)]. Zachowując przyjęte tam oznaczenia będziemy szukali ekstremum funkcji

f(qi , Qz ,    , qn) — h +    +

przy warunku

,    ph Ji ph Ji pin Jn

<?i

<72

4>(qi. Qi» •••» <7») =--1---h... +-

Nie będziemy teraz wprowadzali nowych zmiennych zamiast qi, q₂,..., q_n, tak jak to robiliśmy przedtem, bo nowymi metodami zadanie i tak rozwiązuje się prosto.

Obliczamy różniczkę zupełną obu stron równania 4>=0 i wyznaczamy następnie różniczkę dq„:

dq,

= _ *j.M

Wi(

dqi +... +

ln-Jn

dn-l

-dq,

Podstawiając to wyrażenie do równania df=lidq_l + ...+l„-₁dq„-_l+l„dq„ = 0 otrzymujemy w rezultacie

(

/. J A )

dq 1 + ...+

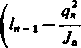
ln~ 1 Jn-l\ dn-l )

dq„

1=0.

Ponieważ różniczki dq_iy dq₂, ...,dq,-_t są już dowolne, współczynniki przy nich muszą być równe zeru, zatem

2 2 2 2

a'“7₂^_"'^_7„TT^_7„ ~ ’

i ostatecznie:

(12)    qi~2\Jji,    qi=2yjJ₂ ,    ..., q„ — X\jj_n -