0461

462

VII. Zastosowania rachunku różniczkowego do geometrii

Gdy parametr t zmienia się, punkt, którego współrzędne określone są tymi równaniami, opisuje rozpatrywaną krzywą. W przypadku przedstawienia krzywej równaniami (9) rolę parametru gra samo x.

Jeżeli w jakimś punkcie krzywej choć jedna z pochodnych x'_t, y\, z, jest różna od zera, to łatwo jest w otoczeniu tego punktu przejść — tak jak i w przypadku krzywej płaskiej — od przedstawienia parametrycznego do przedstawienia równaniami (9). Tylko w otoczeniu punktu osobliwego, w którym wszystkie te pochodne są równe zeru, nie można takiego przejścia zagwarantować.

Również tak jak w przypadku krzywej płaskiej do punktów osobliwych trzeba zaliczyć też tak zwane punkty wielokrotne, tzn. punkty, które się otrzymuje dla dwu lub większej liczby wartości parametru (^Ł).

Przejdziemy teraz do przedstawienia parametrycznego powierzchni.

Określenie położenia punktu na powierzchni wymaga dwóch parametrów — w przypadku przedstawienia równaniami (6) rolę tych parametrów grają dwie współrzędne x i y. Przypuśćmy, że dane są równania

(13)    %=ę(u,v), y = y/(u,v),    z=x(u,v),

w których u i v przybierają wartości z obszaru domkniętego A. Utwórzmy macierz

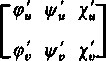
(14)

i załóżmy, że dla u=u₀ i v=v₀ co najmniej jeden z wyznaczników tej macierzy jest różny od zera; np. niech będzie

*0.

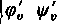
Napiszmy teraz pierwsze dwa z równań (13) w postaci

q>(u,v) — x = 0,    y/(u,v) — y = 0.

Ograniczając się do wartości «, v bliskich u₀ i v₀ możemy na podstawie twierdzenia IV z ustępu 208 powiedzieć, że ten układ dwu równań z czterema zmiennymi x, y, u, v określa zmienne u i v jako jednoznaczne funkcje zmiennych x i y:

u = g(x,y),    v=h(x,y),

ciągłe wraz z pochodnymi. Podstawiając g (*, y) i h(x, y) zamiast u i u do trzeciego z równań (13) otrzymujemy ostatecznie zwykłe przedstawienie powierzchni

z=x(0(x>y),h(x, y))=f(x, y); przy tym funkcja / jest ciągła i ma ciągłe pochodne.

O Patrz notka na dole str. 450.