0457
458
VII. Zastosowania rachunku różniczkowego do geometrii
Dla zbadania zachowania się krzywej w nieskończoności rozpatrzmy odległości punktu krzywej sin#
od osi biegunowej: y=rsia8=a ——, Gdy r-+ ± oo, czyli gdy 8-* ±0, lim y=a. A więc prosta popro-
U
wadzona równolegle do osi biegunowej w odległości a od niej jest asymptotą.
Przykład 3. Spirala logarytmiczna r=aem> (rys. 124).
Jeśli kąt 8 wzrasta (lub maleje) w postępie arytmetycznym, to r rośnie (maleje) w postępie geometrycznym. Odłóżmy na osi biegunowej odcinek OA=a i na prostej prostopadłej do niej odcinek OB-
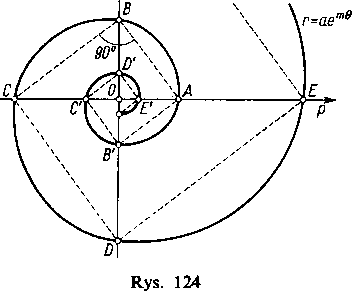
=aem*l2; obydwa punkty A i B leżą na badanej krzywej. Zbudujemy teraz łamaną ABCDE o kątach prostych między ogniwami. Z podobieństwa trójkątów łatwo jest wywnioskować, że odcinki O A, OB, OC, OD, OE, ... tworzą postęp geometryczny o ilorazie em^2, a ponieważ odpowiednie
kąty są równe 0, $iz, 2 ■ łit, 3 ■ Jn.....więc oczywiście
punkty C, D, E, ... także leżą na rozpatrywanej spirali.
Gdy kąt 8 rośnie od 0 do + oo, to punkt obiega nieskończenie wiele razy dokoła bieguna oddalając się przy tym od niego bardzo szybko do nieskończoności ; odległości między zwojami nie są dla tej spirali równe. Kąt 0 może przybierać także wartości ujemne. Gdy 8 dąży do — oo, promień wodzący dąży do 0. Krzywa zakręca się wówczas nieskończenie wiele razy dokoła bieguna przybliżając się do niego nieograniczenie, lecz nigdy go nie osiągając (patrz część AB'C'D'E' ... na rys. 124). Biegun jest więc punktem asymptotycznym krzywej.
Zauważmy, że obracając oś biegunową dokoła bieguna można doprowadzić do zniknięcia czynnika a i sprowadzić równanie spirali logarytmicznej do prostszej postaci r=em>.
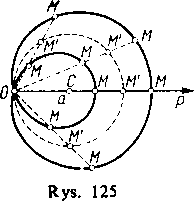
Przykład 4. Ślimaki r=a cos 8+b (rys. 125).
a) M’M=b>a C) M'M=b=a
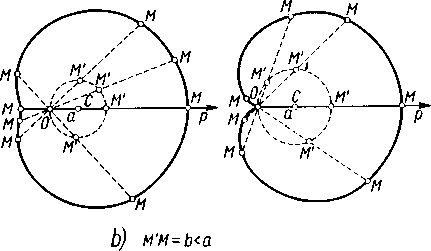
Wyszukiwarka
Podobne podstrony:
498 VII. Zastosowania rachunku różniczkowego do geometrii i dla
462 VII. Zastosowania rachunku różniczkowego do geometrii Gdy parametr t zmienia się, punkt, którego
494 VII. Zastosowania rachunku różniczkowego do geometrii Jeżeli dla x=x0 wstawimy wszędzie w tych
454 VII. Zastosowania rachunku różniczkowego do geometrii a więc np. dla ±0 (czyli dla x-> ±0) po
472 VII. Zastosowania rachunku różniczkowego do geometrii to dla wszystkich tych punktów biegunowa
więcej podobnych podstron