0453

454

VII. Zastosowania rachunku różniczkowego do geometrii

a więc np. dla ±0 (czyli dla x-> ±0) pochodna dyjdx dąży do ±ao. W punkcie/=0 styczna jest zatem pionowa — krzywa ma w tym punkcie ostrze (punkt zwrotu, ustęp 237). To samo można powiedzieć o pozostałych punktach osobliwych.

Przykład 2. Epicykloida i hipocykloida. Jeżeli koło toczy się bez poślizgu po zewnętrznej stronie drugiego koła, to każdy punkt ruchomego okręgu opisuje krzywą zwaną epicykloidą. W przypadku,

gdy toczenie odbywa się od wewnątrz, otrzymuje się hipo-cykloidę. Zajmiemy się wyprowadzeniem równania pierwszej z tych krzywych.

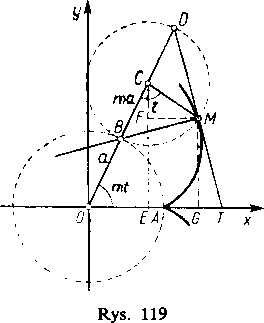
Wybierzmy początek układu w środku O nieruchomego koła, a oś x przeprowadźmy przez to położenie A punktu opisującego krzywą, w którym jest on punktem styczności obu kół (rys. 119). Gdy ruchome koło przetoczy się do nowego położenia pokazanego na rysunku, to punkt A przesunie się do M. Musimy wyznaczyć miejsce geometryczne punktów M.

Oznaczmy przez a promień koła nieruchomego i przez ma promień toczącego się koła. Wybierzmy jako parametr kąt t=$.MCB między promieniem CM łączącym środek toczącego się okręgu z punktem opisującym krzywą a promieniem CB poprowadzonym do punktu styczności. W chwili początkowej kąt ten jest równy zeru.

Wyjaśnimy jak się objawia brak poślizgu. Łuk AB, który przebywa punkt styczności po okręgu nieruchomym, musi być równy łukowi MB przebytemu przez punkt styczności po toczącym się okręgu

a^AOB — ma$.MCB=mat,    skąd %.AOB = mt.

Wyraźmy teraz współrzędne x i y punktu M przez t. Jeśt

x=OG=OE+FM=(a-\-ma) cos mt + ma sin^.FCM, ale

■%.FCM=-%.BCM—$.OCE i *OCE=±n-mt,

tak że

$.FCM^(.l+m)t-łn i sin%FCM= — cos(l +m)t.

Ostatecznie

a [(1 +m) cos mt — m cos(l + m)f ].

Podobnie znajdujemy

y=a l(l+m)sinmt—msin(l-t-m)/].

Równania te dają parametryczne przedstawienie epicykloidy.

Gdy toczący się okrąg zetknie się z nieruchomym okręgiem tym samym swoim punktem, którym się stykał w chwili początkowej, to znaczy rozpatrywanym przez nas punktem opisującym epicykloidę (wówczas t = 2łt), to punkt ten zakończy opisywanie jednej gałęzi krzywej. Przy dalszym toczeniu będzie on opisywał następną gałąź, podobną do pierwszej, itd.

Pochodne

xi— —m(m + l)a [sin/ni—sin(l +m)t], y!=m(m + l)a [cosmf—cos(l +m)t]

są obie jednocześnie równe zeru dla t=2kn (k = 0, ±1, ±2, ...), a więc za każdym razem, gdy punkt opisujący krzywą staje się punktem styczności. Odpowiednie punkty krzywej są osobliwe (punkty zwrotu).