0519

520

VII. Zastosowania rachunku różniczkowego do geometrii

(parametr t występuje w x, y, y'_t, x',) znaleźć obwiednię metodami z ustępu 238 i przekonać się, że pokrywa się ona z ewolutą (10). Można też dowieść, że środek krzywizny jest punktem charakterystycznym na normalnej, to znaczy jest granicznym położeniem punktu przecięcia się tej normalnej z drugą normalną, nieskończenie bliską.

Zajmiemy się teraz lukiem a na ewolucie. Podnosząc równania (11) stronami do kwadratu, dodając i korzystając następnie ze wzoru (11) z ustępu 248 na różniczkę luku otrzymamy

do² = dt² + dri² = dR²,

skąd

(12)    da= ±dR,

czyli (założyliśmy przecież, że <//?# 0):

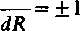
Stosunek ten jest funkcją ciągłą parametru i nie może przeskakiwać od wartości — 1 do wartości +1 nie przybierając wartości pośrednich. Zatem na całym rozpatrywanym łuku musi on być równy jednej z tych liczb. Innymi słowy, z prawej strony równości (12) występuje jeden i ten sam znak (plus lub minus) na całym badanym łuku.

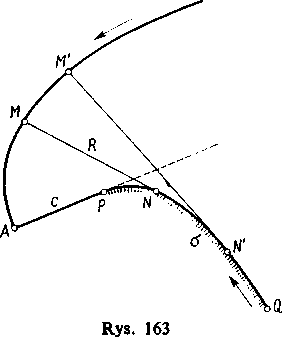
Znak ten zależy od wyboru zwrotu dla liczenia łuku na ewolucie. Jeżeli wybierzemy go tak, żeby łuk a wzrastał razem z promieniem krzywizny R, to we wzorze (12) trzeba brać znak plus; jeżeli zaś przy wzroście łuku a maleje R, to trzeba brać znak minus.

Przypuśćmy, że zachodzi pierwsza z tych dwu możliwości. Wówczas

(13) dR = da, stąd    R — a = c = const.

A więc

2° różnica między promieniem krzywizny i lukiem ewoluty jest stała.

Tym samym różnica między promieniami krzywizny w dwu punktach ewolwenty równa jest łukowi ewoluty między odpowiednimi środkami krzywizn. Wynika stąd, mówiąc nawiasem, interesujący sposób obliczania długości łukli ewoluty.

Znaleziona własność ewoluty ma piękną interpretację mechaniczną. Aby uprościć jej opis, załóżmy, że promień krzywizny R, który nie przybierając wartości równej zeru musi mieć na rozpatrywanym łuku stały znak, jest stale dodatni. Można to zawsze osiągnąć wybierając odpowiednio zwrot przy liczeniu łuku na ewolwencie. Dalej, będziemy liczyli łuk na ewolwencie od tego punktu P, któremu odpowiada najmniejszy promień krzywizny; będzie wówczas też <r>0. Przy tych założeniach stała c występująca w równości (13) jest również dodatnia.