0513

514

VII. Zastosowania rachunku różniczkowego do geometrii

Wobec tego

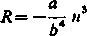
Wiadomo, że połowa parametru 2p dla elipsy i hiperboli wyraża się wzorem p = b¹ja. Wyrażając R przez p i n, otrzymujemy ten sam wzór ostateczny co dla paraboli.

A więc dla wszystkich trzech stożkowych promień krzywizny jest proporcjonalny do sześcianu odcinka normalnej.

10) Na zakończenie powiemy kilka słów o pewnym praktycznym zagadnieniu, w którym właśnie wykorzystuje się w sposób istotny zmianę krzywizny wzdłuż krzywej. Mianowicie chodzi nam o tak zwane krzywe przejściowe, które stosuje się przy wytyczaniu toru kolejowego na zakrętach.

W mechanice dowodzi się, że przy ruchu punktu materialnego po krzywej powstaje siła odśrodkowa, której wielkość wyraża się wzorem

2

mu

F=-;

R

gdzie m jest masą punktu , v — prędkością, a R — promieniem krzywizny krzywej w rozpatrywanym punkcie.

Gdyby prostoliniowy odcinek toru kolejowego przylegał bezpośrednio do zakrętu mającego kształt łuku koła (rys. 159a), to w chwili wjazdu wagonu na ten łuk powstałaby momentalnie siła odśrodkowa

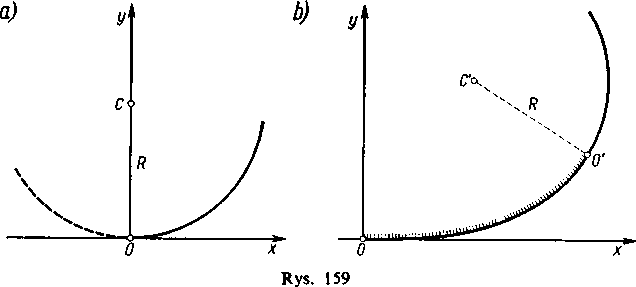
powodując gwałtowny i silny wstrząs szkodliwy dla taboru kolejowego i dla nawierzchni toru. Dla uniknięcia tego łączy się prostoliniową część toru z zakrzywioną za pośrednictwem pewnej krzywej przejściowej (rys. 159b), wzdłuż której promień krzywizny stopniowo maleje od wartości nieskończonej w punkcie zetknięcia się z częścią prostoliniową do wielkości równej promieniowi okręgu — w punkcie zetknięcia się z lukiem okręgu. Siła odśrodkowa rośnie wówczas także stopniowo.

Jako krzywą przejściową stosuje się najczęściej parabolę sześcienną y = x³/6q. W tym wypadku jest

1

dla promienia krzywizny otrzymujemy wyrażenie