053

53

2.4. Rozkłady ciągłe

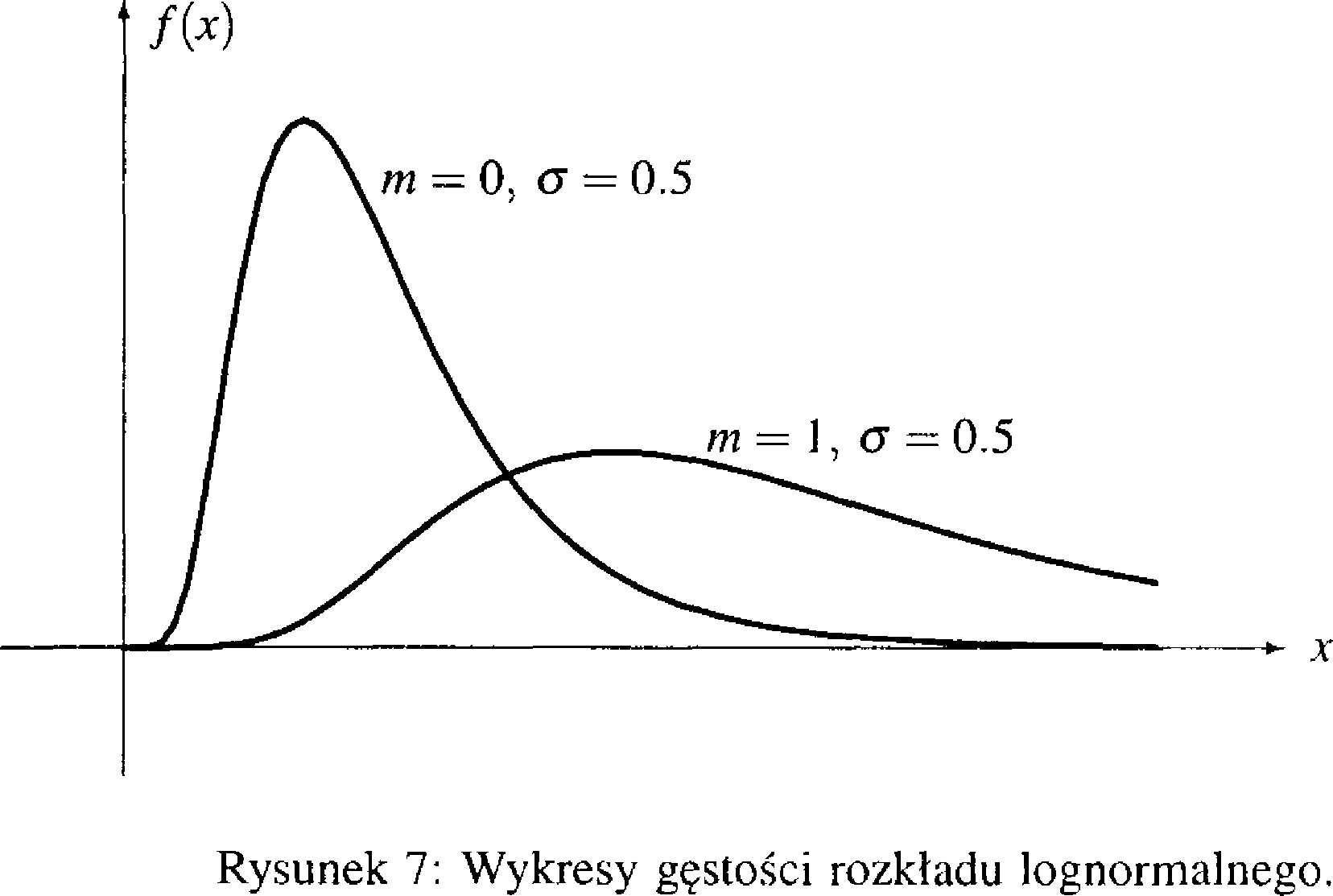
2.4.4. Rozkłady związane z rozkładem normalnym

Rozkład

chi-kwadrat

Niech X;, gdzie i — 1,2, ...,n, będą niezależnymi zmiennymi losowymi o rozkładzie normalnym N(0,1). Zmienną losową %² określa się wzorem:

X²=X²n=Xf+XŹ + ---+XŹ.    (2.4.11)

Mówimy, że zmienna losowa x² określona wzorem (2.4.11) ma rozkład chi-kwadrat Pearsona⁹ o n stopniach swobody.

Ponieważ Xf ma rozkład gamma z parametrami b — p— 1/2 (patrz zadanie 2.5.10), to rozkład chi-kwadrat jest rozkładem gamma z parametrami b — 1/2 i p — n/2.

Zmienna losowa x² przyjmuje tylko wartości dodatnie. Dla małych wartości n rozkład ten jest silnie asymetryczny, a w miarę wzrostu wartości n staje się coraz bardziej zbliżony do rozkładu normalnego (rozkład ten jest asymptotycznie normalny - patrz punkt 3.2.1). Zbieżność rozkładu chi-kwadrat do rozkładu normalnego jest tak szybka, że dla n > 30 dystrybuanta <£>(.v) przybliża dystrybuantę rozkładu chi-kwadrat wystarczająco dobrze. Z tego powodu dla n > 30 zwykle nie ma potrzeby korzystania z tablic rozkładu chi-kwadrat, gdyż wystarczą tablice rozkładu N(0,1). Ze względu na zastosowania w statystyce, w tablicach rozkładu chi-kwadrat podaje się na ogół nie wartości dystrybuanty, a wartości liczb Xa* (wartości krytyczne) dla których zachodzi równość

Pr (r > Xa) = a,    (2.4.12)

^Charles Pearson (1857 - 1936), angielski matematyk, filozof i biolog. Współtwórca współczesnej statystyki.