120027

JB = n•

6    24

Statystyka JB ma rozkład chi-kwadrat o dwóch stopniach swobody.

W tablicy rozkładu clii-kwadrat dla dwóch stopni swobody, przy poziomie istotności 0,05 odczytuje się wartość krytyczną równą 5,991

Obszar krytyczny jest prawostronny, wiec przy JB>5,991 odrzuca się hipotezę o normalności rozkładu składnika losowego.

Przykład

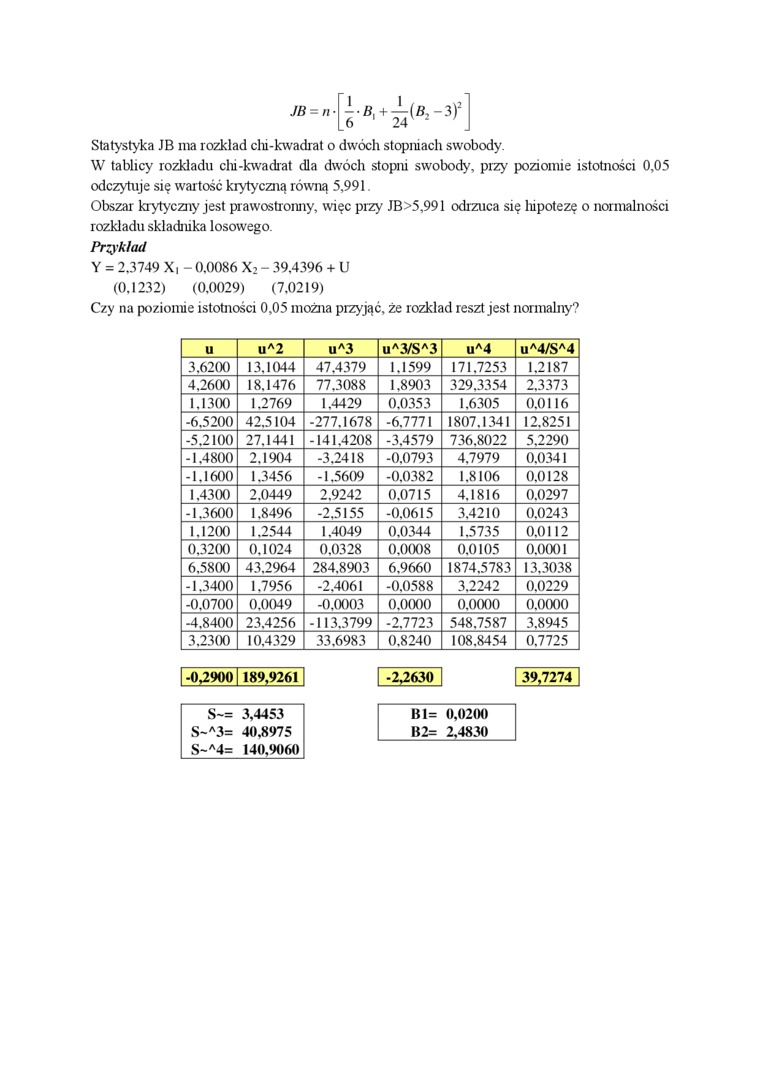
Y = 2,3749 X, - 0,0086 X₂ - 39,4396 + U (0,1232)    (0,0029)    (7,0219)

Czy na poziomie istotności 0,05 można przyjąć, że rozkład reszt jest normalny?

u	c > K>	u^A3	u^A3/S^A3	u^A4	u^A4/S^A4
3,6200	13,1044	47.4379	1.1599	171.7253	1.2187
4,2600	18,1476	77.3088	1.8903	329,3354	2.3373
1,1300	1,2769	1,4429	0.0353	1,6305	0.0116
-6.5200	42,5104	-277.1678	-6.7771	1807.1341	12.8251
-5,2100	27.1441	-141.4208	-3.4579	736,8022	5.2290
-1.4800	2.1904	-3.2418	-0.0793	4.7979	0.0341
-1,1600	1.3456	-1,5609	-0,0382	1,8106	0,0128
1,4300	2.0449	2.9242	0.0715	4.1816	0.0297
-1.3600	1.8496	-2,5155	-0.0615	3,4210	0,0243
1,1200	1,2544	1,4049	0,0344	1,5735	0,0112
0,3200	0,1024	0,0328	().(KK)8	0,0105	0.0001
6,5800	43,2964	284.8903	6.9660	1874.5783	13.3038
-1.3400	1.7956	-2.4061	-0.0588	3,2242	0.0229
-0.0700	0,0049	-0,0003	0,0000	0,0000	0.0000
-4.8400	23.4256	-113.3799	-2.7723	548.7587	3.8945
3,2300	10,4329	33.6983	0.8240	108,8454	0,7725

1 -0,29001189,92611

1 -2,2630 |    | 39,7274 |

S~= 3,4453 S~^A3= 40,8975 S-^A4= 140,9060

Bl= 0,0200

B2= 2,4830