Matematyka 2 D3

442 VI Elementy statystyki maicmatwznej_

2)    Z tablic rozkład chi-kwadrat dla jednego stopnia swobody odczytujemy kwanty I Xw.9j=3.84

3)    Budujemy prawostronny zbiór krytyczny K,*, ,=<3.84;x).

Ponieważ xin_P ⁼ l*6gK,,₀₅=^<3,84;x)_l więc zaobserwowana liczba

braków w 100-elcmemowej próbce nic przeczy' zapewnieniom dostawy, że wadliwość jego tow aru wynosi tylko 6%.    ■

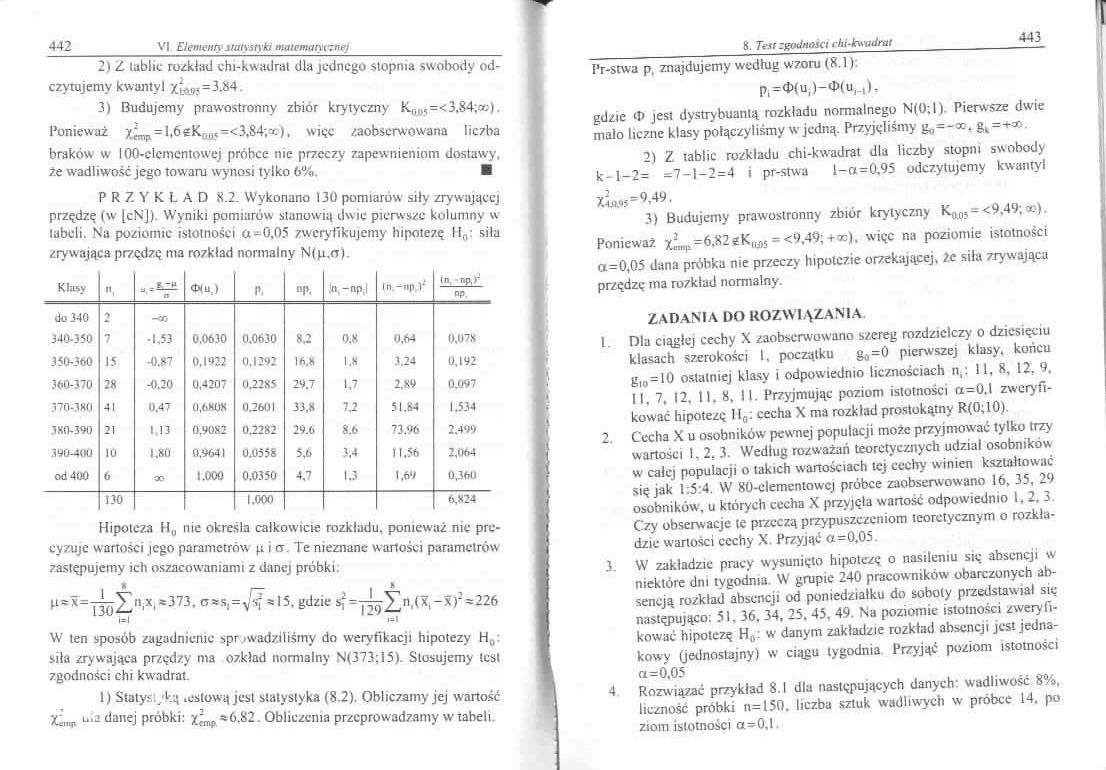
PRZYKŁAD 8.2. Wykonano 130 pomiarów siły zrywającej przędzę (w (cNJ). Wyniki pomiarów stanowią dwie pierwsze kulumny w tabeli. Na poziomie istotności a-0.05 zweryfikujemy hipotezę ll₀: siła zrywająca przędzę ma rozkład normalny N(p.rr).

Klasy	n,	n	<Wu.)	P,	np,	.'n,—npd	In -np,V’	In np,r np.
do 340	2	-00
340-350	7	-1.53	0.0630	0.0630	8.2	0.8	0.64	0,078
350-360	15	-0.87	0,1922	0.1292	16.8	1,8	3.24	U. 192
360-370	28	-0.20	0.4207	0,22X5	29.7	1,7	2.89	0.097
.170-3X0	41	0.47	0.6X08	0,2601	33,8	U	51.84	1.534
3X0-390	21	1,13	0.90X2	0.22X2	29.6	8.6	73.96	2.499
390-400	10	1.80	0.9641	0.0558	5.6	3.4	11.56	2,064
od 400	6	00	1.000	0.0350	4,7	1.3	1.69	0.360
	130			1.000				6.824

Hipoteza ll„ nie określa całkowicie rozkładu, ponieważ nie precyzuje w artości jego parametrów p i rr. Te nieznane w artości parametrów zastępujemy ich oszacowaniami z danej próbki;

I *    r~    \ *

i=l    wl

W ten sposób zagadnienie sprowadziliśmy do weryfikacji hipotezy H₀: siła zrywająca przędzy ma ozkład normalny N(373;15). Stosujemy test zgodności chi kwadrat.

1) Statys.yką testową jest statystyka (8.2). Obliczamy jej wartość XL* ^uia danej próbki: x«_mp *6.82. Obliczenia przeprowadzamy w tabeli.

Pr-stwa p. znajdujemy według wzoru (8.1):

PjS^Uij-OłU,.,), gdzie ‘P jesi dystrybuanlą rozkładu normalnego N(0;1). Pierwsze dwie mało liczne klasy połączyliśmy w jedną. Przyjęliśmy g_1l=-'Oc. g_k=-r*>

2)    Z tablic rozkładu chi-kwadrat dla liczby stopni swobody k-1—2= =7 — 1—2=4 i pr-stwa l-ct=0.95 odczytujemy kwantyl

X4A«5 ~ ^9 *

3)    Budujemy prawostronny zbiór krytyczny K₀₀,= <9.49; x) Ponieważ xLr.⁼6_ł82«K_ujM = <9.49; +x). więc na poziomie istotności a=0,05 dana próbka me przeczy hipotezie orzekającej, źe siła zrywająca przędzę ma rozkład normalny.

ZADANIA DO ROZWIĄZANIA.

I. Dla ciągłej cechy X zaobserwowano szereg rozdzielczy o dziesięciu klasach szerokości I, początku g_tl=0 pierwszej klasy, końcu g_lo=10 ostatniej klasy i odpowiednio lic/nościach n,: 11, 8, 12. 9. II. 7, 12, II. 8. II Przyjmując poziom istotności rx=O.I zweryfikować hipotezę ll₀: cecha X ma rozkład prostokątny R(0;10).

2 Cecha X u osobników pewnej populacji może przyjmować tylko trzy wartości I. 2, 3. Według rozważań teoretycznych udział osobników w całej populacji o takich wartościach tej cechy winien kształtować się jak 1:5:4. W 80-clemcntowcj próbce zaobserwowano ló. 35, 29 osobników, u których cecha X przyjęła wartość odpowiednio l, 2. 3 Czy obserwacje te przeczą przypuszczeniom teoretycznym o rozkładzie wartości cechy X Przyjąć a=0.05 3. W zakładzie pracy wysunięto hipotezę o nasileniu się absencji w niektóre dni tygodnia. W grupie 240 pracowników obarczonych absencją rozkład absencji od poniedziałku do soboty przedstawiał się następująco: 51, 36. 34, 25. 45. 49. Na poziomie istotności zweryfikować hipotezę H₀: w danym zakładzie rozkład absencji jest jednakowy (jednostajny) w ciągu tygodnia Przyjąć poziom istotności a=0,05

4 Rozwiązać przykład 8.1 dla następujących danych: wadliwość 8%. hcznośc próbki n=150. liczba sztuk wadliwych w próbce 14. po zioin istotności a=0.1